Stichwörter: Mischungsregeln, Mischngen, mischbar, mehrphasige Systeme, Viskosität, Normalspannung
RH095-DE
EINFÜHRUNG POYMERMISCHUNGEN
Komplexe Polymersysteme sind Kombinationen von verschiedenen Polymertypen zu ein- oder mehrphasigen Systemen. Die einzelnen Komponenten werden zusammengestellt, sei es um die Kosten zu verringern, Verarbeitungseigenschaften oder mechanischen Eigenschaften zu verbessern. Einer der Hauptgründe für der Erstellung von Mischungen sind jedoch die Herstellungskosten. Polymerkombinationen bestehend aus einer teueren und einer preisgünstigeren Komponente haben hochwertigere Eigenschaften bei niedrigerem Preis. Polymere werden oft gemischt um die spezifischen Eigenschaften zweier Komponenten zu vereinen. Kristalline und amorphe Materialien sind ein Beispiel. Amorphe Polymere sind transparent und haben eine bessere Formbeständigkeit, kristalline Polymer haben einen höheren Modul und sind steifer.
Die Mischung von Thermoplasten mit Elastomeren erzeugt Materialien mit hoher Festigkeit und guter Schlagzähigkeit. Durch Mischen können neue Eigenschaften erzeugt werden, ohne neue Materialien zu entwickeln.
How to Develop Complex Polymer Combinations?
Der einfachste Weg Polymere zu veränderen besteht darin feste Partikel oder Faser beizugeben. Diese Zusätze verstärken das Material und erhöhen den Modul und die Festigkeit.
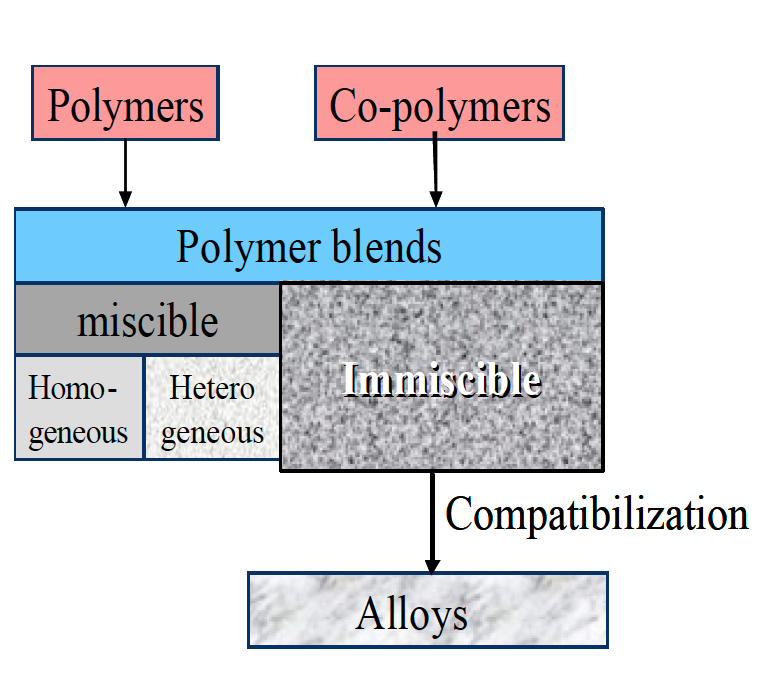
Das Zusammenführen von chemisch verschiedenen Polymeren in einem Mischungsprozess, erweitert die Palette der möglichen Eigenschaften erheblich. Polymere Materialmischungen sich mischbar oder auch nicht (Abbildung 1). Mischbare Systeme können aus chemisch gleichen (homologen) oder verschiedenen (heterogenen) Komponenten bestehen. Nicht mischbare Polymerkombinationen sind mehrphasige Systeme. Die Eigenschaften lassen sich zusätzlich durch Kompa tibilisierung wie z. B. die Zugabe von Co-Polymeren veränderen.
Warum können Polymere gemischt werden – oder auch nicht?
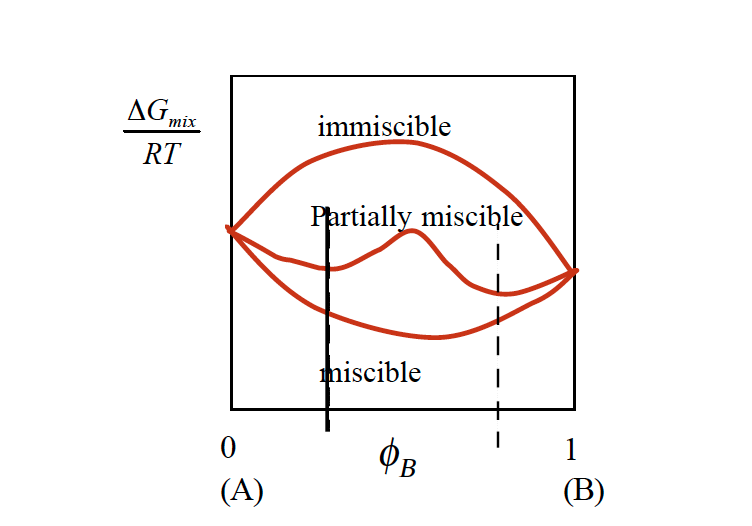
Ob Polymer sich spontan mischen oder nicht bestimmt die Gibbs Freien Enthalpie. Ist diese negative, dann mischen sich die Polymere makroskopisch und bilden eine einzige Phase.
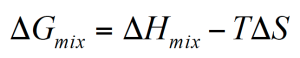
Die meisten Polymermischungen sind nicht mischbar. Die Ursache ist die Entropie in der Gleichung 1, welche wenig zur Freien Enthalpie beiträgt. Polymere sind meist ungeordnete Systeme und die Zugabe von fremden Polymerketten verändert die Unordnung nur unwesentlich. Die Mischungsenthalpie muß dann negativ sein damit sich die Polymerkomponenten spontan mischen. Viele Polymerkombinationen sind bei kleinem Anteil der dispersen Phase mischbar, bei höherer Konzentration jedoch nicht. Dabei spielt die Temperatur natürlich eine wichtige Rolle. Solche Polymermischungem werden teil-mischbar genannt (Abbildung 2).
Eigenschaften von Polymermischungen
Bei der Kombination von Polymeren ist es sehr wichtig zu verstehen, wie sich die Materialeigenschaften mit der Zusammensetzung veränderen. Ein Hauptziel der Produktentwicklung ist es Mischungsregeln zu entwickeln um die Produkt-eigenschaften vorhersagen zu können. Diese Mischungsregeln sind selten lineare Beziehungen. Mischungen können z. B. synergetisch sein, das heißt die gewünschte Eigenschaft steigt überproportional mit dem Volumenanteil der minderen Komponente an oder nicht synergetisch wenn dieselbe Eigenschaft sich verschlechtert (Abbildung 3). Die allgemeine Form der Mischungsregel besteht aus den zwei Termen welche den Beitrag jeder Komponente beschreiben, sowie einen Wechselwirkungsterm.
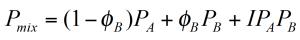
φB ist der Volumenanteil der geringeren Komponente B. Typische Materialeigenschaften sind die Viskosität, die Glasübergangstemperatur Tg oder auch jede andere mechanische oder physika-lische Eigenschaft. Für nicht mischbare Systeme, können die Mischungsregeln wegen des starken Einflußes der Morphologie sehr komplex werden.

DIE RHEOLOGIE HOMOLOGER MISCHUNGEN
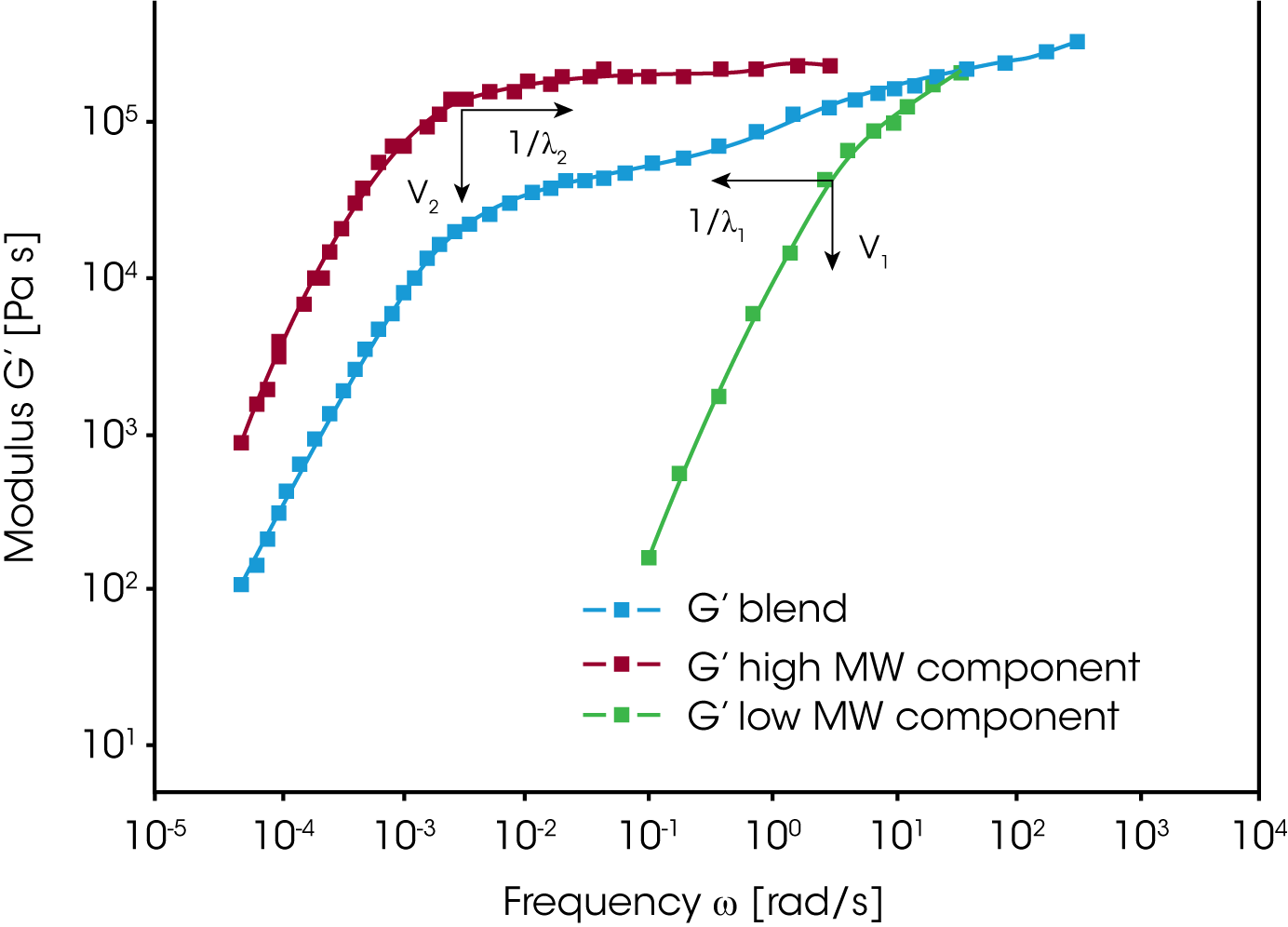
Homopolymere werden oft gemischt um die Viskosität und die Elastizität der Polymerschmelze einzustellen. Auf dieselbe Weise kann der Einfluss der Länge der Polymerkette auf das rheologische Verhalten bestimmt werden. Der Speichermodul der binären Mischung in Abbildung 4 zeigt den Beitrag der zwei Polymerkomponenten deutlich. Der Terminalbereich der Mischung befindet sich zwischen den Fließbereichen der einzelnen Komponenten. Dies bedeutet, daß die Relaxationszeiten der hochmolekularen Komponente verringert und diejenigen der nieder-molekularen Komponente erhöht werden. Der Volumenanteil bestimmt die Höhe des Plateauwertes. Der Modul bzw. das Relaxationszeitspektrum der Mischung zweier monodispersen Homopolymeren kann als Funktion des Mischungsverhältnisses und eines Verschiebungsfaktors für die einzelnen Komponenten beschrieben werden wie folgt:
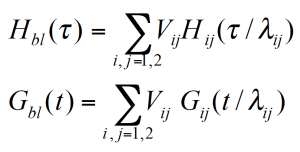
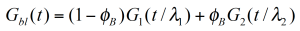
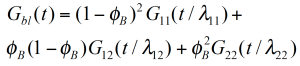
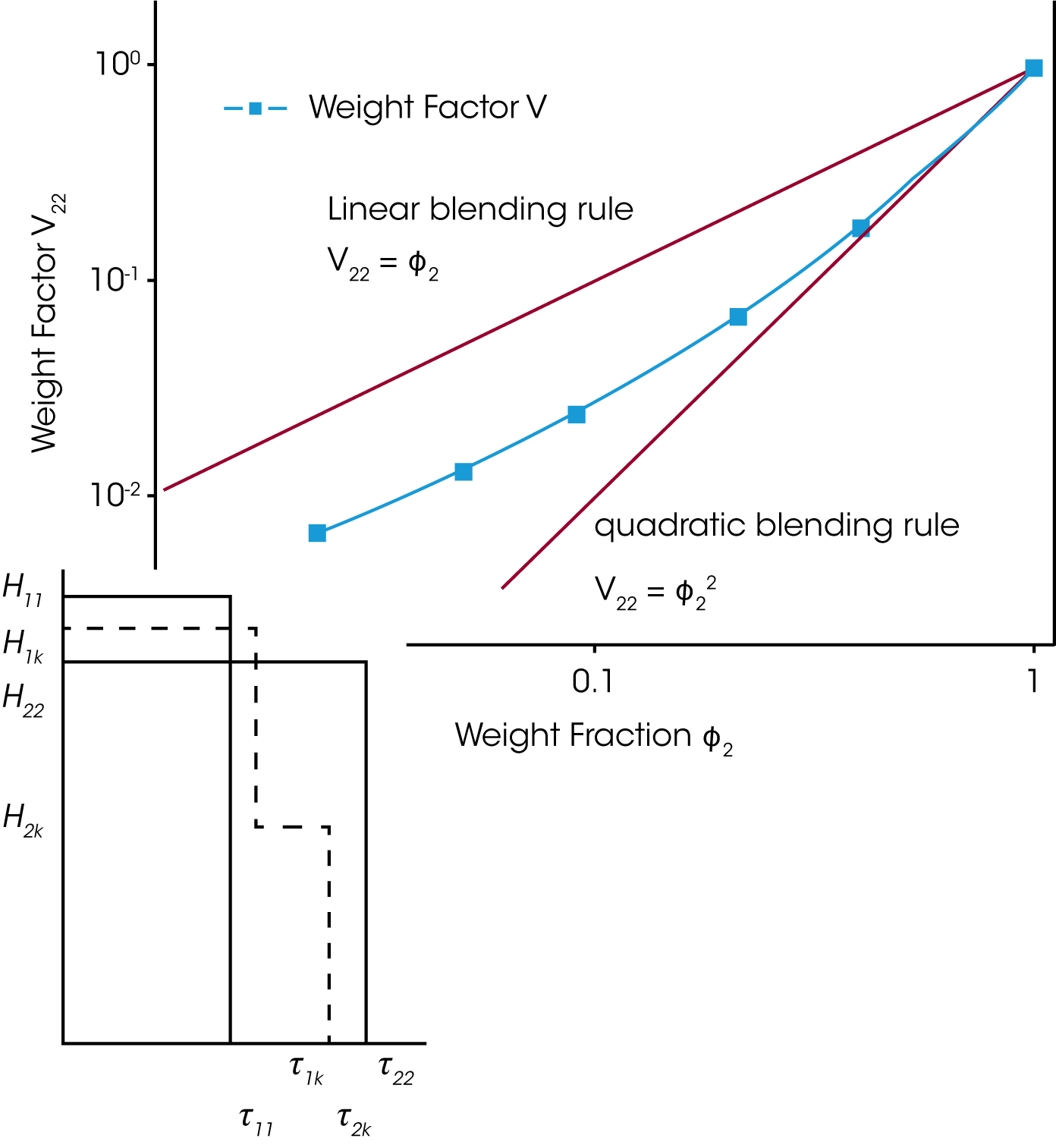
Für eine binäre Mischung mit φB, dem Volumenanteil der hochmolekularen Komponente ist die Beziehung für ein empirisches, lineares und quadratisches Mischungsgesetzt in Gleichung (4) und (5) gegeben. Um die Gültigkeit dieser einfachen Mischungsgesetze zu prüfen ist der experimentell bestimmte Gewichtungsfaktor V22 als Funktion des Gewichtsanteils der hochmolekularen Kompnenten in Abbildung 5 dargestellt. V22 wurde aus dem Relaxationszeitspektrums bei Zugrundlegung einer einfachen Kastenverteilung bestimmt. /1/ Es ist ersichtlich, daß die experimentellen Daten zwischen denen eines reinen linearen und quadratischen Mischungsgetzes liegen. Die Verschiebungsfaktoren ʎ11 und ʎ22 sind abhängig von dem Gewichtsanteils ɸB. Zusätzlich korreliert ʎ22 mit MZ was bedeutet, daß die hochmolekulare Komponente einen stärkeren Einfluß auf das rheologische Verhalten der Mischung hat /1/.
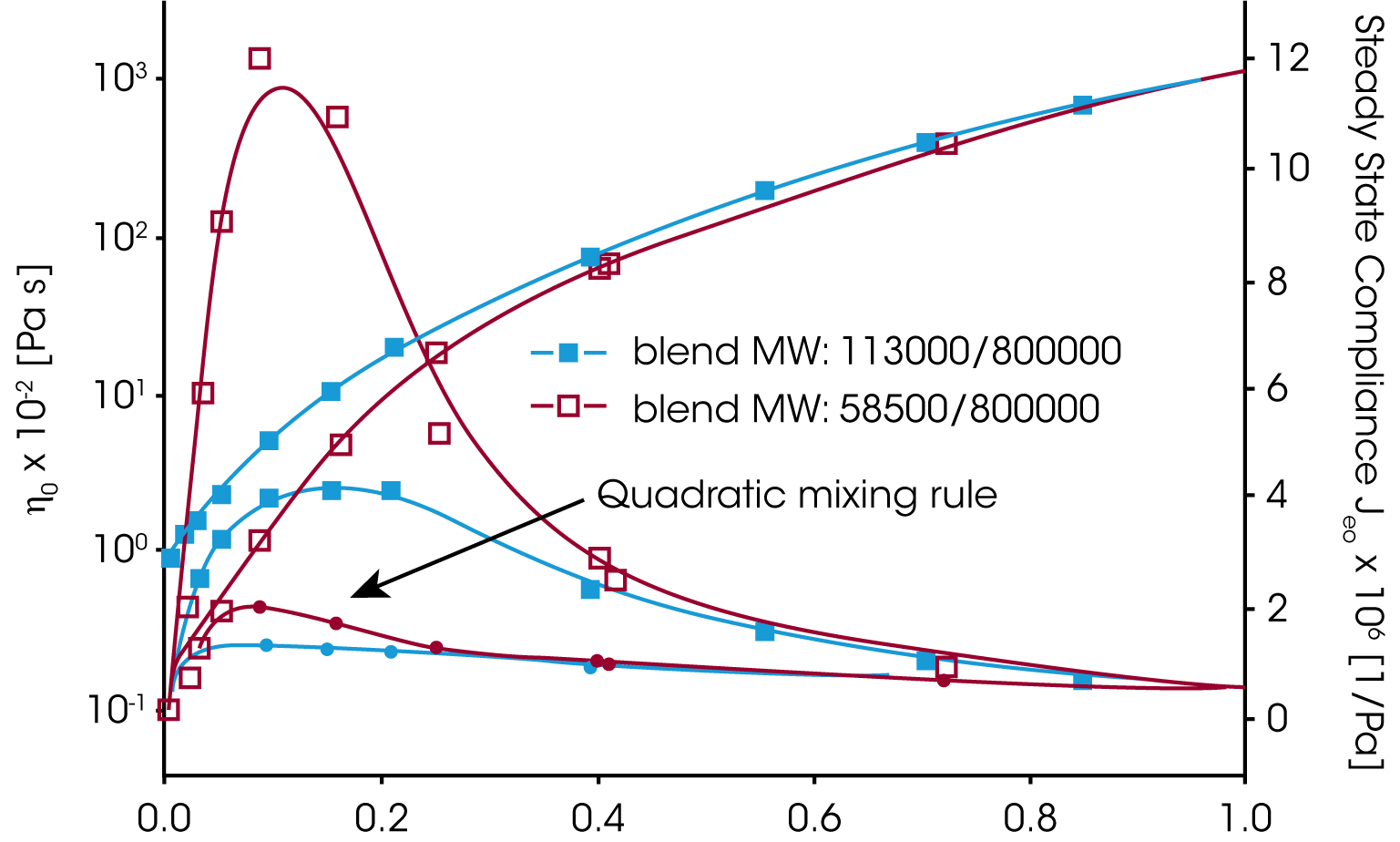
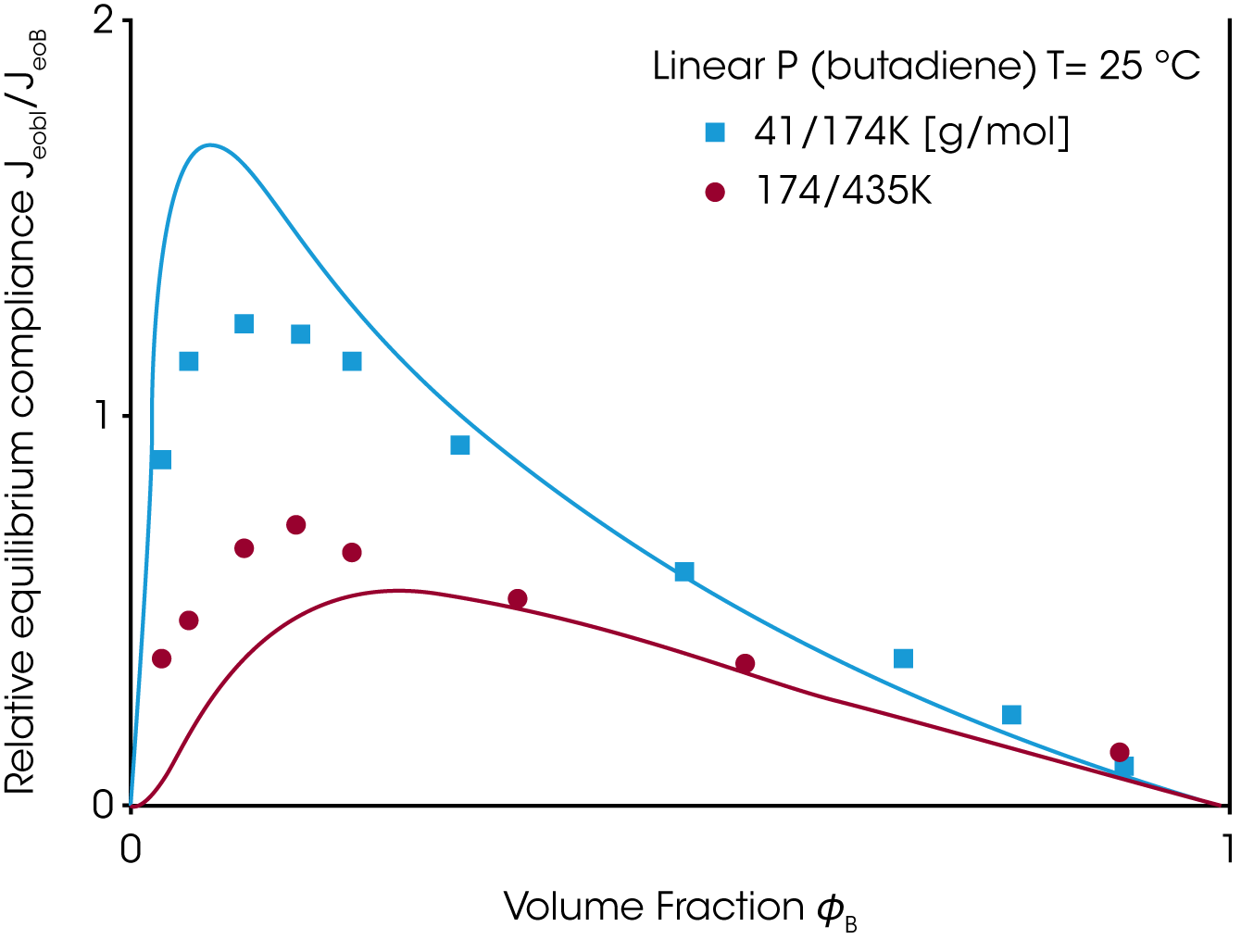
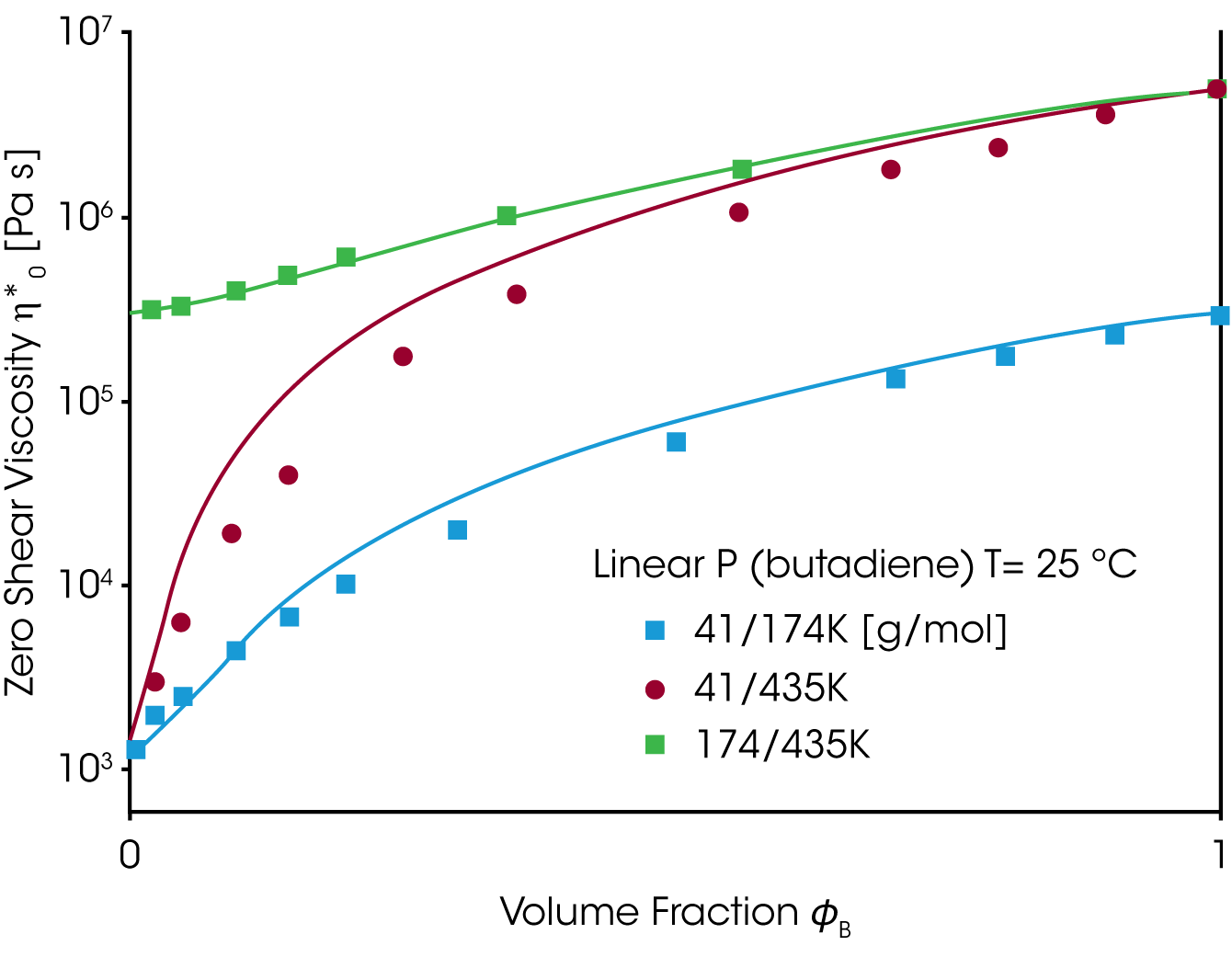
Geeignete Materialgrößen um das Mischungsgesetzt zu überprüfen sind die Nullviskosität ƞo und die stationäre Gleichgewichtsnachgiebigkeit Jeo. Während die Viskosität mit dem Gewichsanteil der hochmolekularen Komponente ansteigt, geht die Gleichgewichtsnachgiebigkeit durch ein Maximum bei kleinem Anteil der hochmolekularen Komponente ɸB (Abbildung 6). Weder das einfache noch das quadratische Mischungsgesetz beschreiben den experimentellen Verlauf der stationären Gleichgewichtsnachgiebigkeit und der Nullviskosität.
Basierend auf dem Schlauchmodel (Reptationsmodel) /2,3/ hat Tsenoglou folgendes Mischungsgesetz für den Modul und die Viskisität hergeleitet:
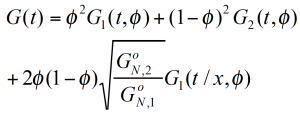
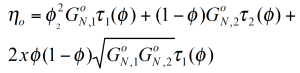
Das Mischungsgesetzt ist quadratisch im Bezug auf den Gewichtsanteil und schließt einen komplexen Wechselwirkungsterm ein. τ1 und τ2 sind die monodisperse Relaxations- (Reptations-) zeiten der zwei Konponenten der Mischung /2/. z ist ein lokaler Reibungsfaktor und Me das Verschlaufungsmolekulargewicht.
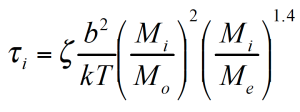
Die Nullviskosität und die stationäre Gleichgewichtsnachgiebigkeit als Funktion des Gewichtsanteils werden wesentlich besser mit diesem modifizierten Mischungsgesetz beschrieben, wie in Abbildung 7 ersichtlich.
Das Mischungsgesetz von Tsenoglou wurde erweitert /4/ und der Gewichtsanteil der hochmolekularen Kompnente durch die Molekulargewichtsverteilung w(M) ersetzt. Das erweiterte Mischungsgesetz wird eingesetzt um die Molekulargewichtsverteilung aus experimentellen rheologischen Daten zu bestimmen. Abbildung 8 zeigt die Molekulargewichtsverteilung einer bimodalen Mischung zweier engverteilter Polystyrole mit unterschiedlichem Molekulargewicht, berechnet aus dem Relaxationszeitspektrum bzw. dem dynamischen Speichermodul G’ und Verlustmodul G’’ /5/. Zum Vergleich sind GPC Daten mit aufgetragen. Gute Übereinstimmung zwischen GPC und rheologischen Daten konnte in diesem Fall erzielt werden.
DIE RHEOLOGIE HETEROGENER MISCHBARER POLYMERMISCHUNGEN
Heterogene Polymersysteme bestehen aus Polymeren unterschiedlicher chemischer Natur und Glasübergangstemperatur Tg. Komplet mischbare heterogene Polymersysteme haben nur einen Glasübergang, welcher zwischen denjenigen der Komponenten liegt. Typische mischbare Systeme sind Mischungen von PS/PVME (Polystyrol/ Poly(vinyl methyl ether)), PSAN/PMMA (Poly (styrol acrylnitril)/Poly(methyl methacrylat)), PEO/PMMA (Poly(ethylene oxid) /Poly(methyl methacrylat)), PB/PIP (Polybutadien/Polyisopren), usw.
Mischbare heterogene Mischungen folgen nicht den Mischungsregeln welche für homologe Mischungen erstellt wurden. Obwohl diese auch nur eine Glasübergangstemperatur Tg aufweisen wie homologe Mischungsreihen, ist Tg stark abhängig von der Zusammensetzung, der Glasübergang ist asymmetrisch und breiter als der Übergang derreinen Komponenten. Heterogene Mischungen folgen nicht dem Zeit-Temperatursuperpostionsprinzip und sind somit thermo-rheologisch komplexe Systeme.
Bedingt durch den Zusammenschluß der Monomere über kovalente Bindungen entlang der Hauptkette entstehen lokale Konzentrationsfluktuationen der Komponenten gleicher chemischer Natur /6/, wie in Abbildung 9 dargestellt. Diese sogenannte Selbstkonzentration ist definiert als das Volumen eines Kuhnelementes dividiert durch die Länge eines Kuhnelements hoch drei. Da Polymere mit niedrigerem Tg flexibler sind, haben sie eine höhere Selbstkonzentration (ɸs für PI=0.45) als Polymere mit höherem Tg. Deshalb verhalten sich Polymerkomponenten in der Mischung lokal so wie in der reinen Phase. Folglich ist die molekulare Beweglichkeit und die Dynamik der Segmente in einer Mischung nicht nur temperatur- sondern auch konzentrationsabhängig.
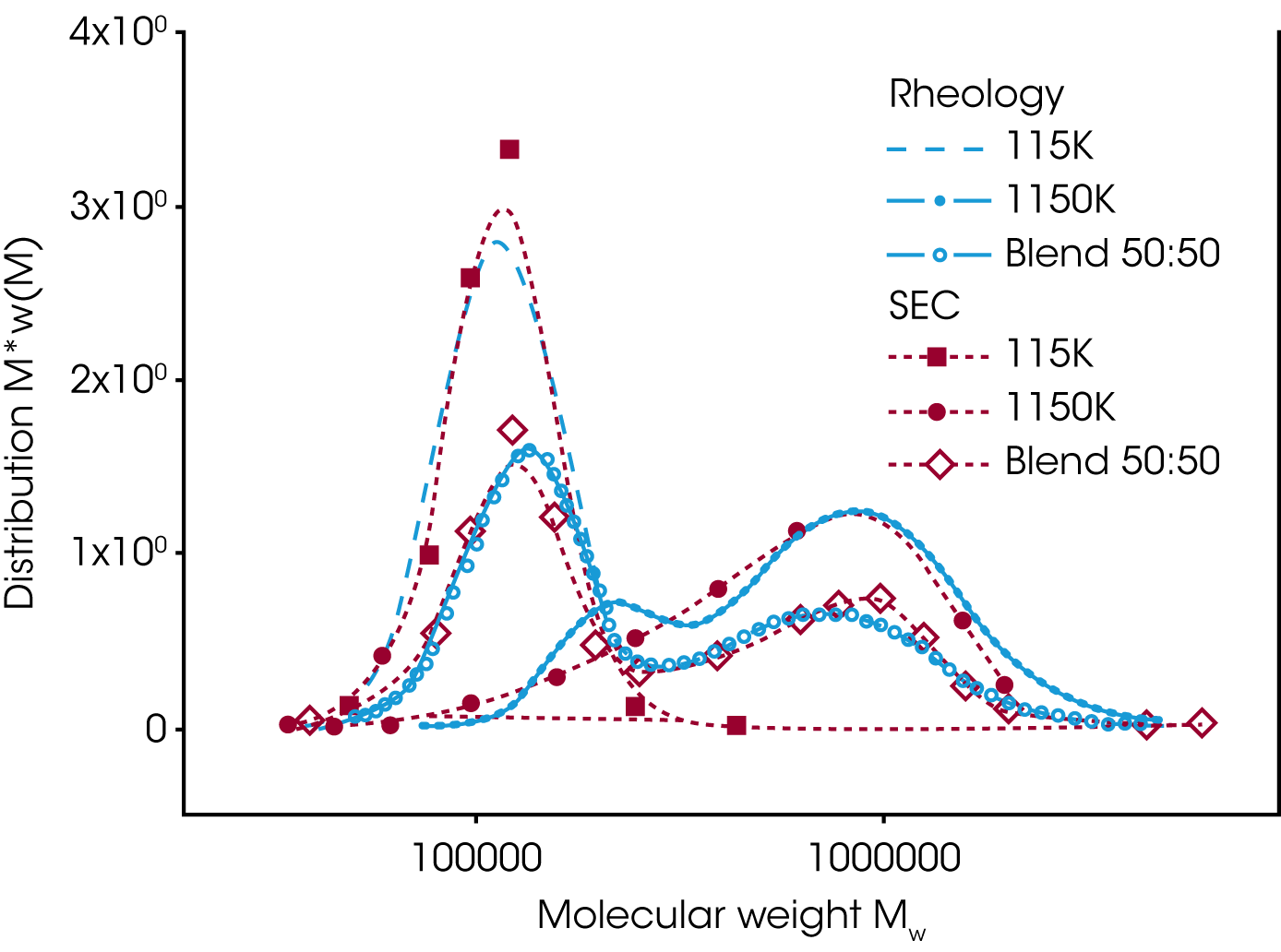
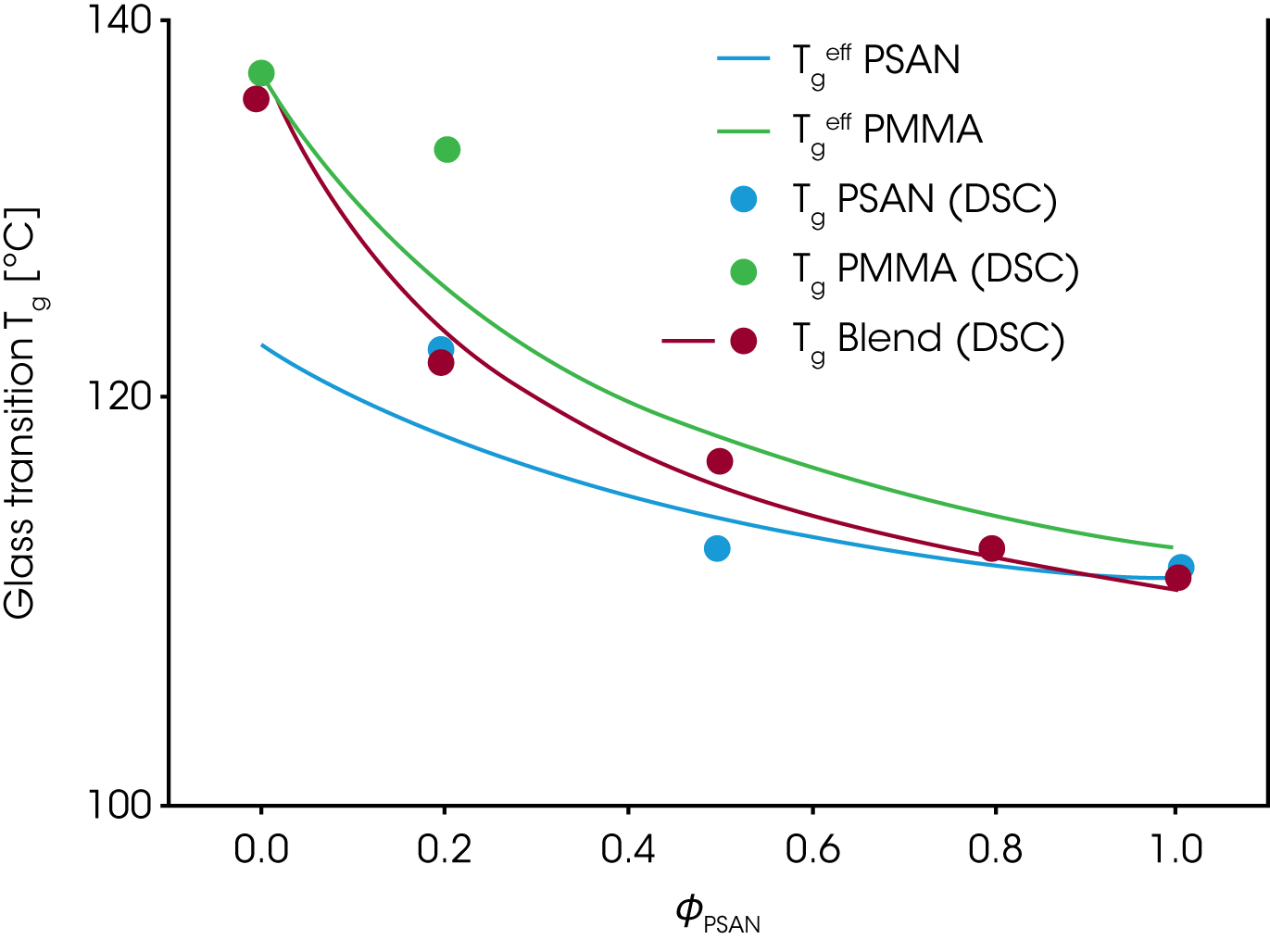
Abbildung 10 zeigt den mittels DSC ermittelten Glasübergang als Funktion der Zusammensetzung Tg(ɸ) einer PMMA/PSAN Mischung. Die einhüllenden Kurven entsprechen dem effektiven Glasübergang Tgeff welcher dem Tg bei der effektiven lokalen Konzentration ɸeff entspricht und wie folgt aus der mittleren Konzentration und der Selbstkonzentration ɸs berechnet wird:
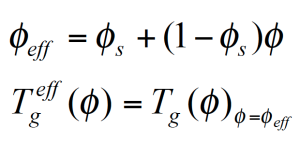
Da die Polymerkomponente mit niedrigerem Tg flexibler ist, die Selbstkonzentration ɸs dadurch höher wird und die Kettendynamik mehr derjenigen des reinen Polymers entspricht wird die lokale Glasübergangstemperatur Tgeff erniedrigt im Vergleich zum gemessenen Tg der Mischung.
Die Komponenten mit dem höheren Tg Wert haben eine niedrigere Selbstkonzentration ɸs und die lokale Beweglichkeit entspricht mehr derjenigen der Mischung selbst. Deshalb ist Tgeff dieser Komponente dem Tg der Mischung ähnlich. Als Folge der lokalen Veränderungen von Tg mit dem Volumenanteil, verbreitert sich der gemessene Glasübergang mit abnehmender Konzentration von PSAN in der Mischung.
Als Folge der lokalen Konzentrationsveränderungen, verändert sich der Reibungsfaktor wie folgt:
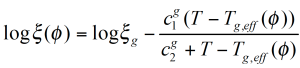
ζ ist hier nicht nur eine Funktion der Temperatur, sondern auch der lokalen Konzentration der Komponenten. Die mittlere Relaxationszeit (Reptationszeit) muß in Gleichung 8 /7/ für jede Komponente mit dem neuen Reibungsfaktor angepaßt werden. Das mittlere Molekulargewicht zwischen Verschlaufungen bei gegebenem Volumenanteil ɸ berechnet sich aus den einzelnen Komponenten wie folgt:
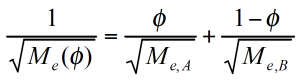
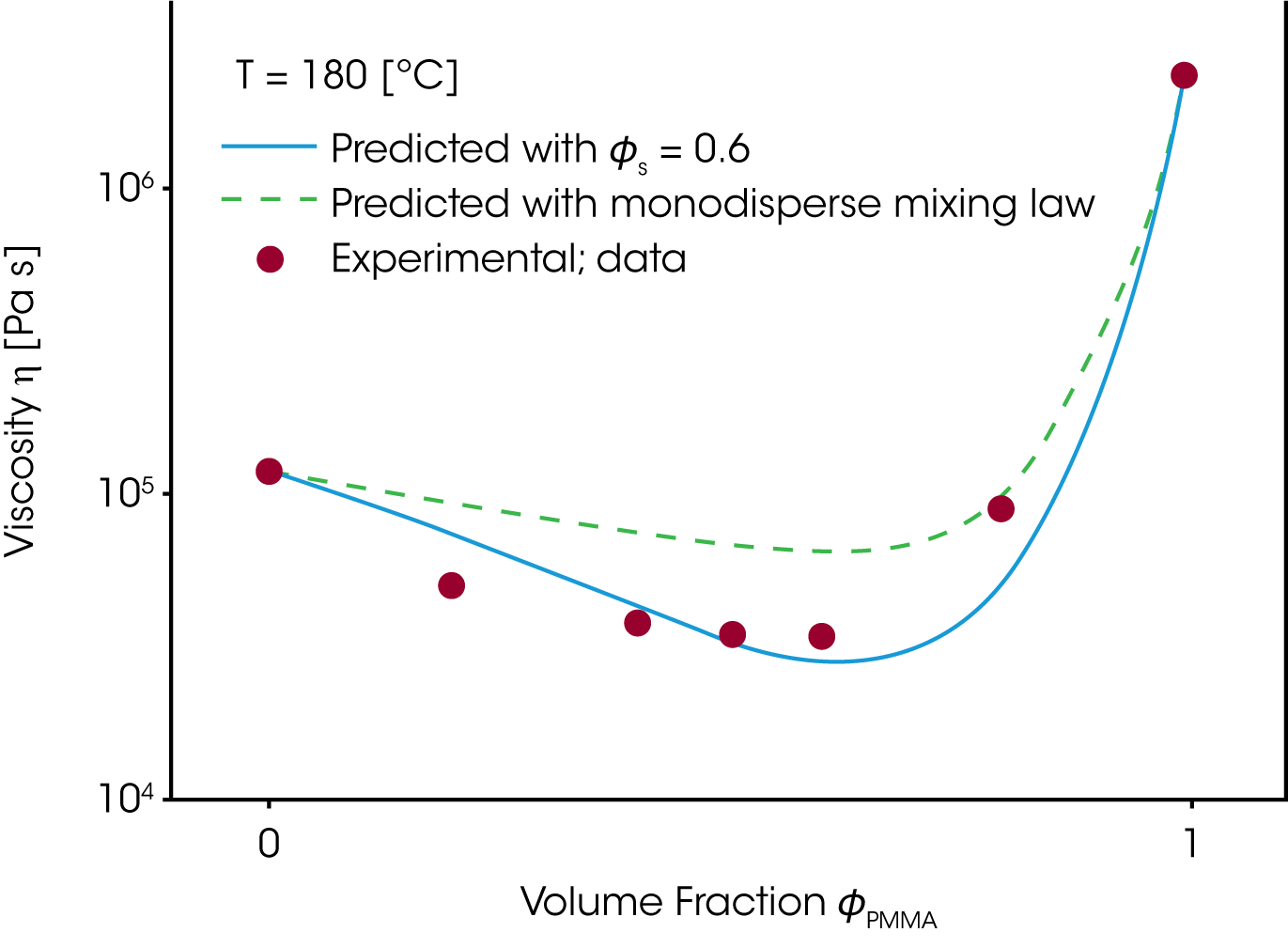
Die Zeitkonstanten der zwei Komponenten A und B werden im Mischungsgesetz nach Tsenoglou, welches für homologe Polymersysteme entwickelt wurde ersetzt und das rheologische Verhalten als Funktion der relativen Konzentration berechnet. Die Viskosität der PMMA/PEO Mischung (Abbildung 11) wurde für einen Selbstkonzentrationswert von ɸs = 0.6 berechnet. PEO ist ein flexibles Monomer, was sich im hohen Wert für die Selbstkonzentration wiederspiegelt. /8/.
DIE RHEOLOGIE NICHT MISCHBARER POLYMERSYSTEME
Die meisten Polymermischungen sind nicht kompatibel und somit nicht mischbar. Sie sind mehrphasig und weisen meistens eine recht komplexe Morphologie auf. Um die geeigneten mechanischen Eigenschaften zu erhalten, müssen nicht mischbare Polymersysteme modifiziert (Kompatibilisierung) werden wie z. B. durch Zugabe von Co-Polymeren um die Adhäsion an der Phasengrenze zu verbessern. Sowohl der zugegebene Kompatibilisator als auch die Fließprozesse während der Herstellung stabilisieren die Morphologie und verbesseren somit die physikalischen Eigenschaften von komplexen Polymersystemen. Physikalische Eigenschaften wie Oberflächeneigenschaften, Zähigkeit, Dimensionsstabilität, Gasdurchlässigkeit, usw. können über die Morphologie eingestellt werden
Dynamisch mechanische Verhalten von PS/ PMMA Mischungen
Ein einfaches Beispiel eines nicht mischbaren Systems ist die PMMA/PS Kombination. In dieser Untersuchung ist /9/ PMMA die kontinuierliche und PS die disperse Phase welche in Form kleiner Einschlüsse vorliegt. Die Mischung wurde durch Mischen im Extruder hergestellt.
Die PS und PMMA Komponenten wurden auf Ihre Ähnlichkeit in Bezug auf das Frequenzspektrum (Relaxationszeitspektrum) ausgewählt.
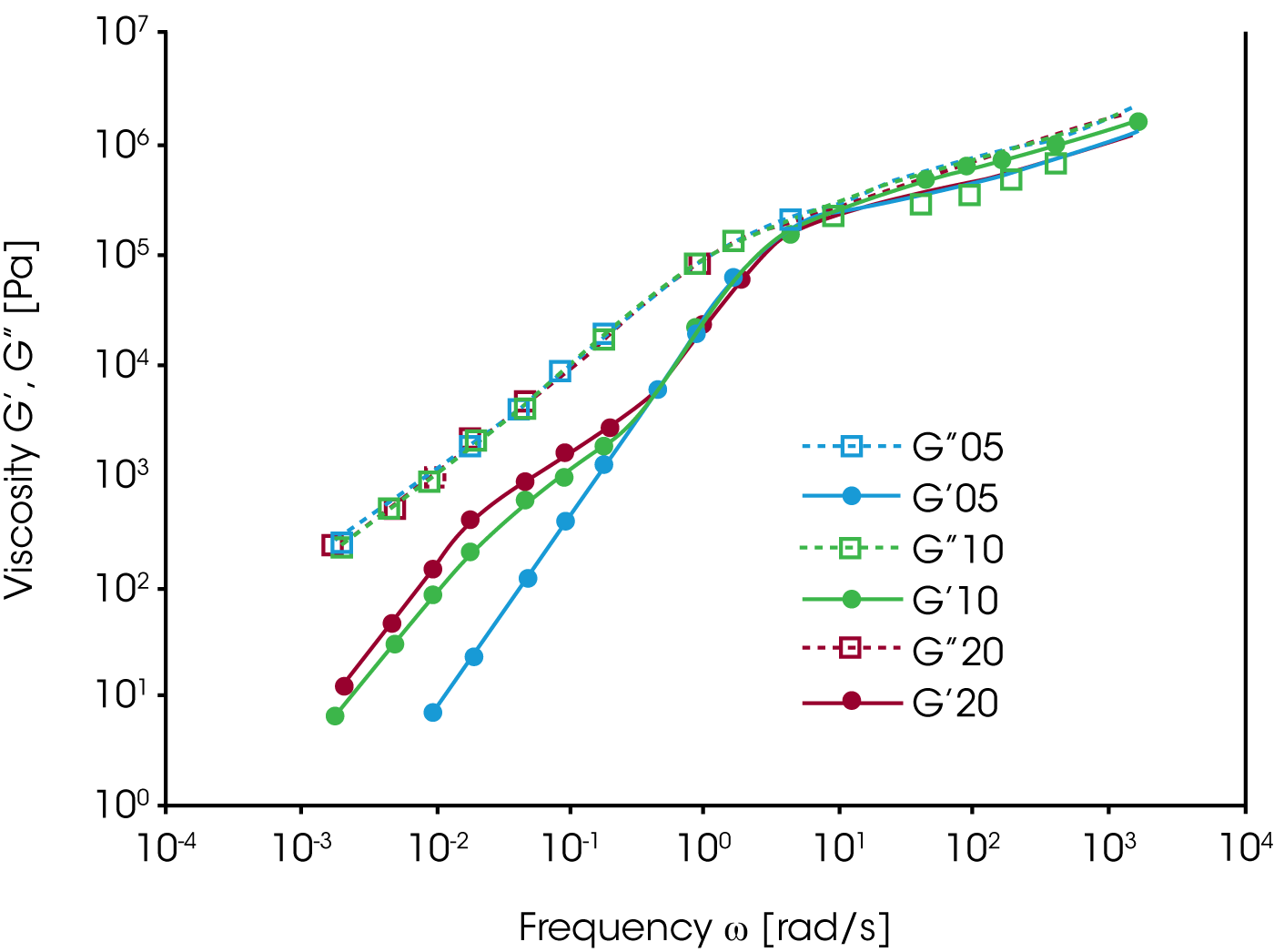
Mischungen mit 5, 10 und 20% PS Anteil wurden rheologisch auf Ihre Frequenzabhänigkeit im Oszillationsversuch untersucht. Der Speichermodul G‘ in Abbildung 12 zeigt eine auffallende, starke Relaxation (Schulter bei kleiner Frequenz) auf, welche mit wachsendem Anteil der dispersen Phase zunimmt. Die Größe dieser Relaxation korrelieret mit dem Volumenanteil der PS Phase.
TEM (Transmission Elektronen Mikroskopie) Untersuchungen zeigen eine Zunahme der Domaingröße der dispersen Phase sowie ein Verbreiterung der Größenverteilung mit zunehmendem PS Anteil auf. Die starke Zunahme der Elastizität der Mischung, charakterisiert durch die Schulter in G’ bei kleiner Frequenz, ist auf Speicherung von mechanischer Energie in der Grenzfläche bei der Deformation der sphärischen Einschlüsse zurückzuführen. Die gespeicherte Energie wird bei der Formrelaxation der PS Einschlüsse wieder dissipiert. Die langsame Relaxation der Morphologie im Vergleich zur Relaxation der Polymerketten erlaubt deren Abtrennung wie im folgenden gezeigt wird. Der Mechnismus der Energiespeicherung ist die Zunahme der Oberflächenenergie mit zunehmender Phasengrenze, die Energiedissipation ist die Reibung an der Grenzfläche.
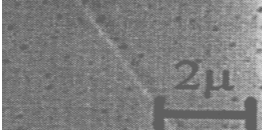


Können diese experimentellen Erkentnisse in Mischungregeln berücksichtigt werden um das rheologische Verhalten nicht mischbarer Polymersysteme vorherzusagen? Betrachten wir dazu das einfachste mehrphasige System, eine feste Kugel in einer Newtonischen Flüssigkeit. Laut Einstein / 10/ ist die Viskositätszunahme in einem solchen System ein rein hydrodynamischer Effekt und nur vom Volumenanteil der dispersen Phase abhängig. Werden die festen Kugeln durch deformierbare Tropfen, welche mit einer Newtonischen Flüssigkeit gefüllt sind ersetzt, dann verhält sich das System wie eine viskoelastische Flüssigkeit mit einer Relaxationszeit, gegeben durch die Viskosität der kontinuierlichen Phase und der Grenzflächenspannung. Das Emulsionsmodel von Choi and Schowalter /11/ beschreibt den Verlauf der Viskosität und der Normalspannung zweier nicht mischbarer Newtonischer Flüssigkeiten als Funktion der Zusammensetzung. Für nicht mischbare Polymersysteme kann das Mischungsgesetz mit einem Term für die Form-relaxation der dispersen Phase wie folgt angeschrieben werden:
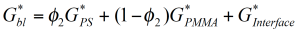
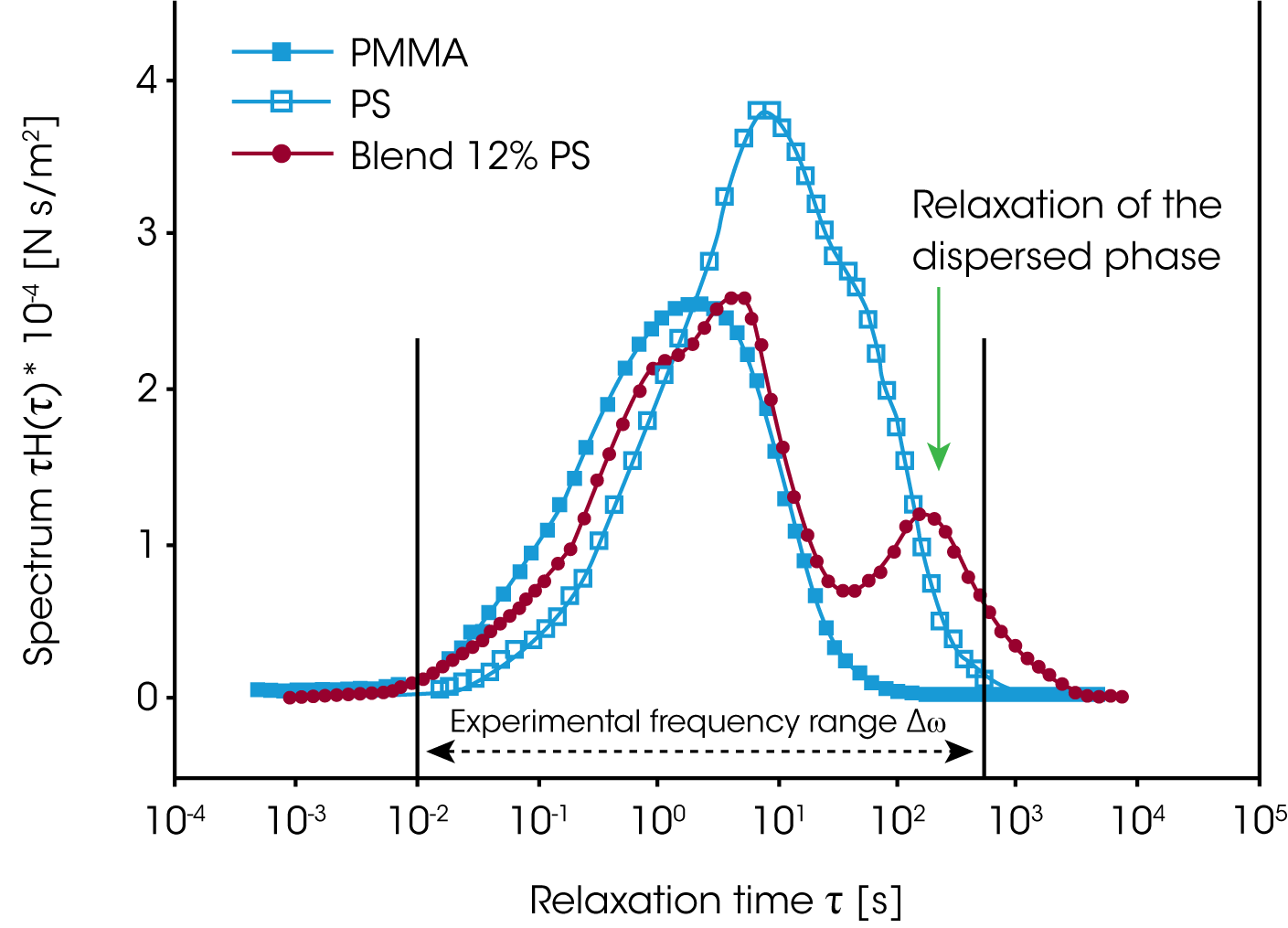
Bei den hier untersuchten PMMA/PS Mischun gen ist die Phasenrelaxation wesentlich langsamer als die Kettenrelaxation der Komponenten. Gramespacher und al. /12/ haben das Relaxationszeitspektrum aus den experimentellen dynamischen Moduli G’ und G” bestimmt und die, mit der Relaxationszeit gewichteten Spektren τH(lnτ), in Abbildung 13 miteinander verglichen. Die Mischung zeigt ein ausgeprägtes zweites Maximum im Vergleich zu den reinen Komponenten auf. Eine charakteristische Relaxationszeit für die Phasenrelaxation wurde aus dem zweiten Maximum bestimmt und die Grenzflächenspannung wie folgt hergeleitet:
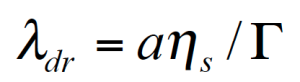
a ist hier die Tropfengröße. Um die Tropfengröße zu bestimmen muß die Grenzflächenspannung bekannt sein oder the Grenzflächenspannung kann berechnet werden, wenn die mittlere Tropfengröße (z.B. aus Lichtstreuung) zur Verfügung steht.
Verfolgen der Tropfengröße mittels Rheologie im Scherfeld
Nicht mischbare Polymersysteme können nur mit großem Energieaufwand bis auf die mikroskopische Ebene gemischt werden. Die mechanische Energie zum Mischen und zum Unterbinden von Koaleszenz kann z. B. im Extruder zugeführt werden. Die sich einstellende Tropfengröße ist abhängig von der zugeführten Energiemenge, den Strömungsbedingungen usw. Kann die Rheologie eingesetzt werden um den Verlauf der Tropfengröße unter vorgegebenen Strömungsverhältnissen zu verfolgen und zu beobachten?
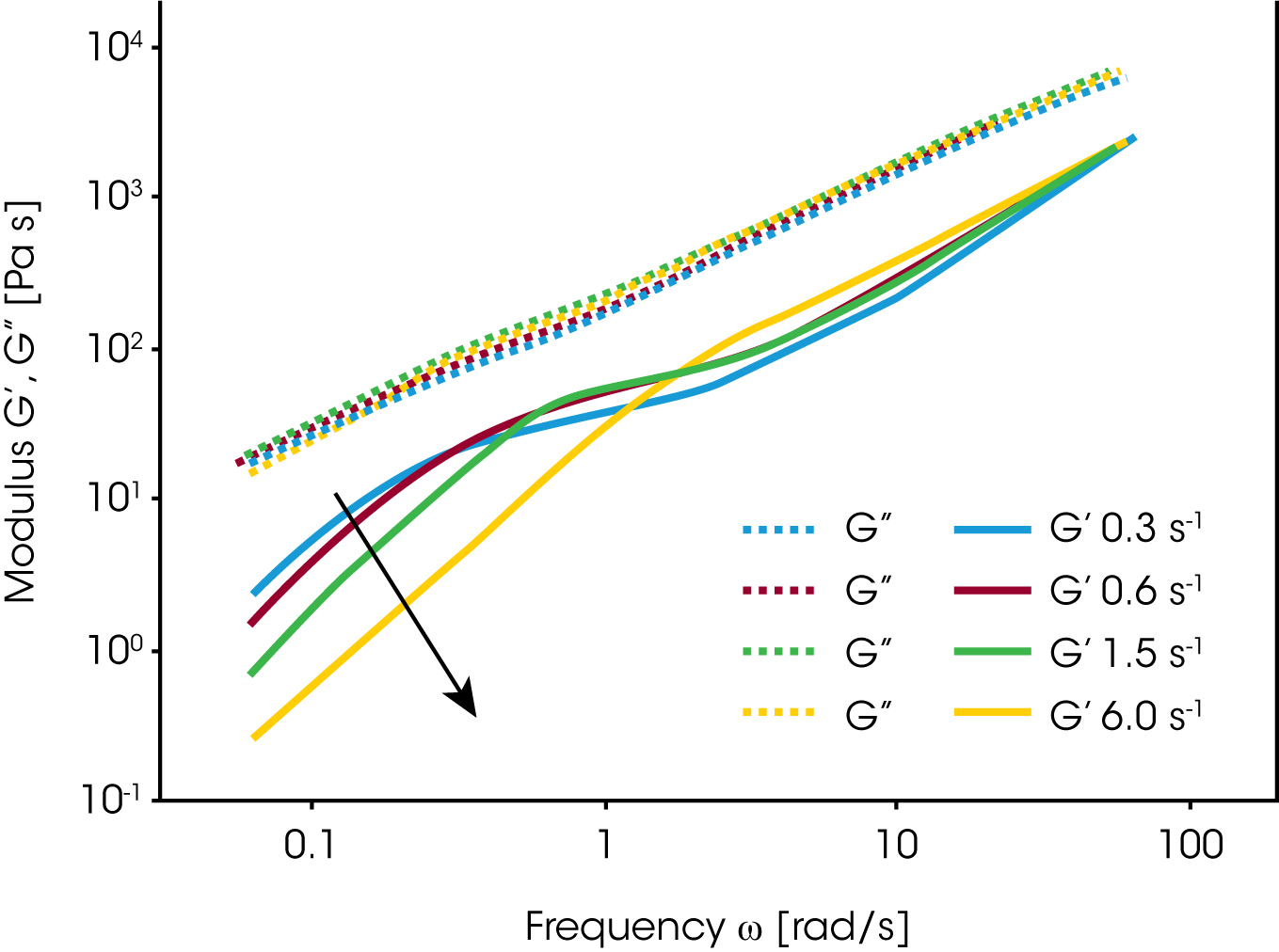
Vinckier und al./13 / haben das nicht mischbare Polymersystem PDMS und PIB (70/30) in Oszillation als Funktion einer aufgebrachten Vorscherung untersucht. In Bild 14 zeigt der Speichermodul bei kleiner Frequenz einen maximalen Wert nach Vorscheren mit der kleinsten Scherrate. Unter diesen Bedingunen sind die dispergierten PIB Tropfen groß und die Grenzfläche kann dementsprechend viel Energie speichern. Mit zunehmender Scherrate jedoch nimmt der elastische Betrag sowie G’ ab. Dies wird durch eine Abnahme der Partikelgröße erklärt. Palierne /14/ hat 1990 ein erweitertes Emulsionsmodel für viskoelastische Flüssigkeiten vorgeschlagen. Graebling /15/ hat daraus folgende Gleichung für einen mittleren Tropfenradius hergeleitet:
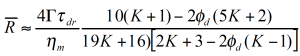
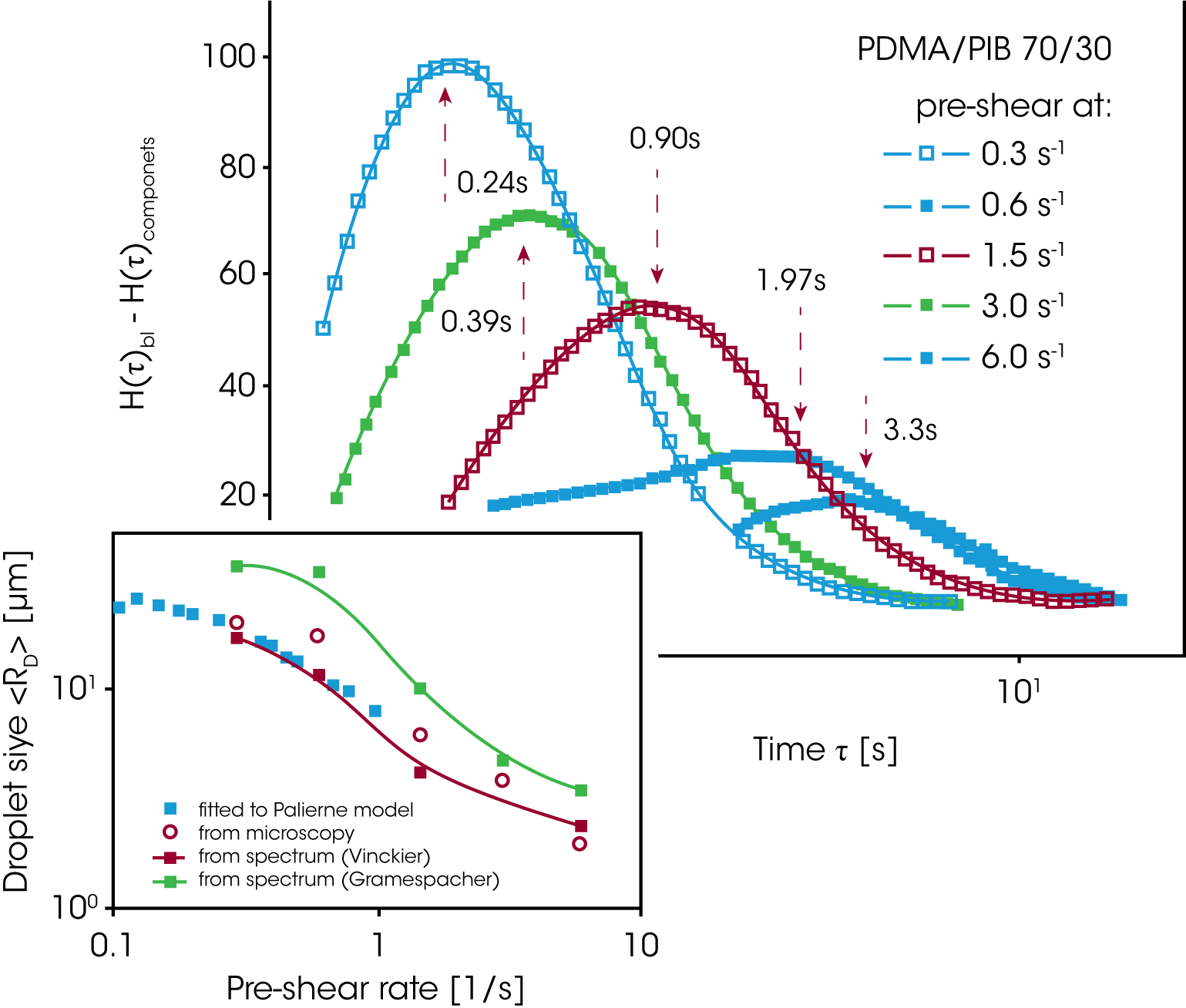
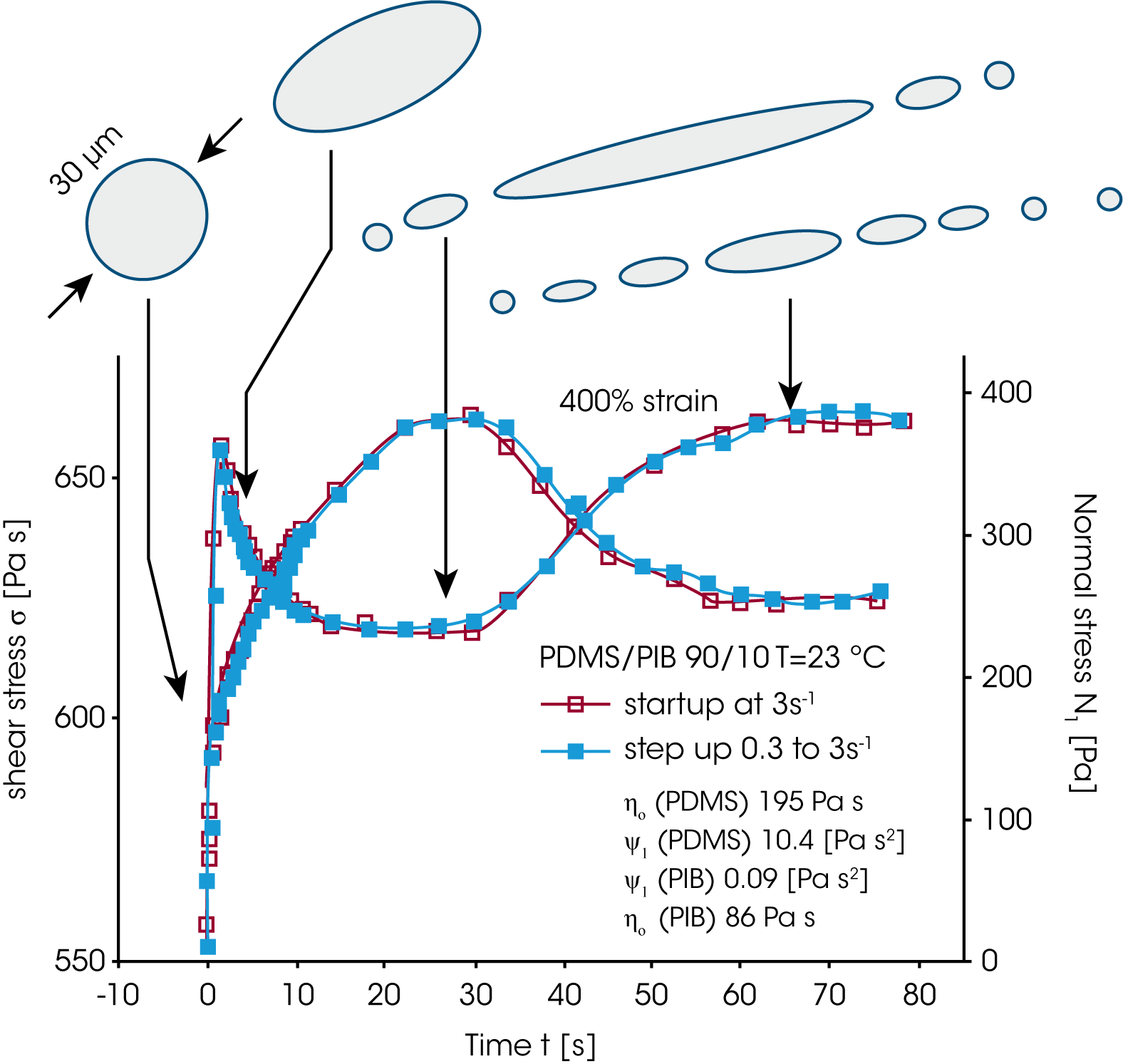
In Bild 15 sind die Relaxationszeitspektren der Oszillationsmessungen aus Abbildung 14 dargestellt. Der Effekt der Phasenrelaxation wurde isoliert indem die Beiträge der reinen Komponenten zum gemessenen Relaxationszeitspektrums linear abgezogen wurden. Der aus Gleichung 14 berechnete Tropfenradius (Bild 15) nimmt um eine Zehnerpotenz ab, bedingt durch das Aufbrechen der Tropfen bei den höheren Scherraten. Vinckier und al. /16/ haben ebenfalls die zeitabhängige Viskosität und die Normalspannung im Spannversuch gemessen (Abbildung 16). Im Spannversuch geht die Viskosität sofort durch ein spitzes Maximum, fällt auf einen Minimum um dann langsam einen Gleichgewichtswert zu erreichen. Die Normalspannung verläuft entgegengesetzt, erreicht ein Maximum wenn die Viskosität das Minimum durchschreitet und fällt dann auf einen Gleichgewichtswert ab. Geht man davon aus, daß die dispergierte Phase aus sphärischen Kugeln besteht die unter dem Einfluß der Scherung zu einer Ellipsoide verformt werden, dann muß die Viskosität abnehmen weil die dispergierte Phase dem Fließen einen geringeren Wiederstand entgegensetzt. Die Phasendeformation speichert Energie in der wachsenden Grenzfläche, folgedessen muß die Normalspannung (Elastizität) zunehmen. Ist das Maximum in der Normalspannung erreicht, brechen die Tropen auf und bilden kleinere Tröpfchen – die Normalkraft nimmt jetzt ab und die Viskosität nimmt zu, da eine größere Anzahl kleiner Tropfen den Fließwiderstand wieder erhöht. Ein Gleichgewichtzustand und eine konstante mittlere Tropfengröße stellen sich mit der Zeit langsam ein.
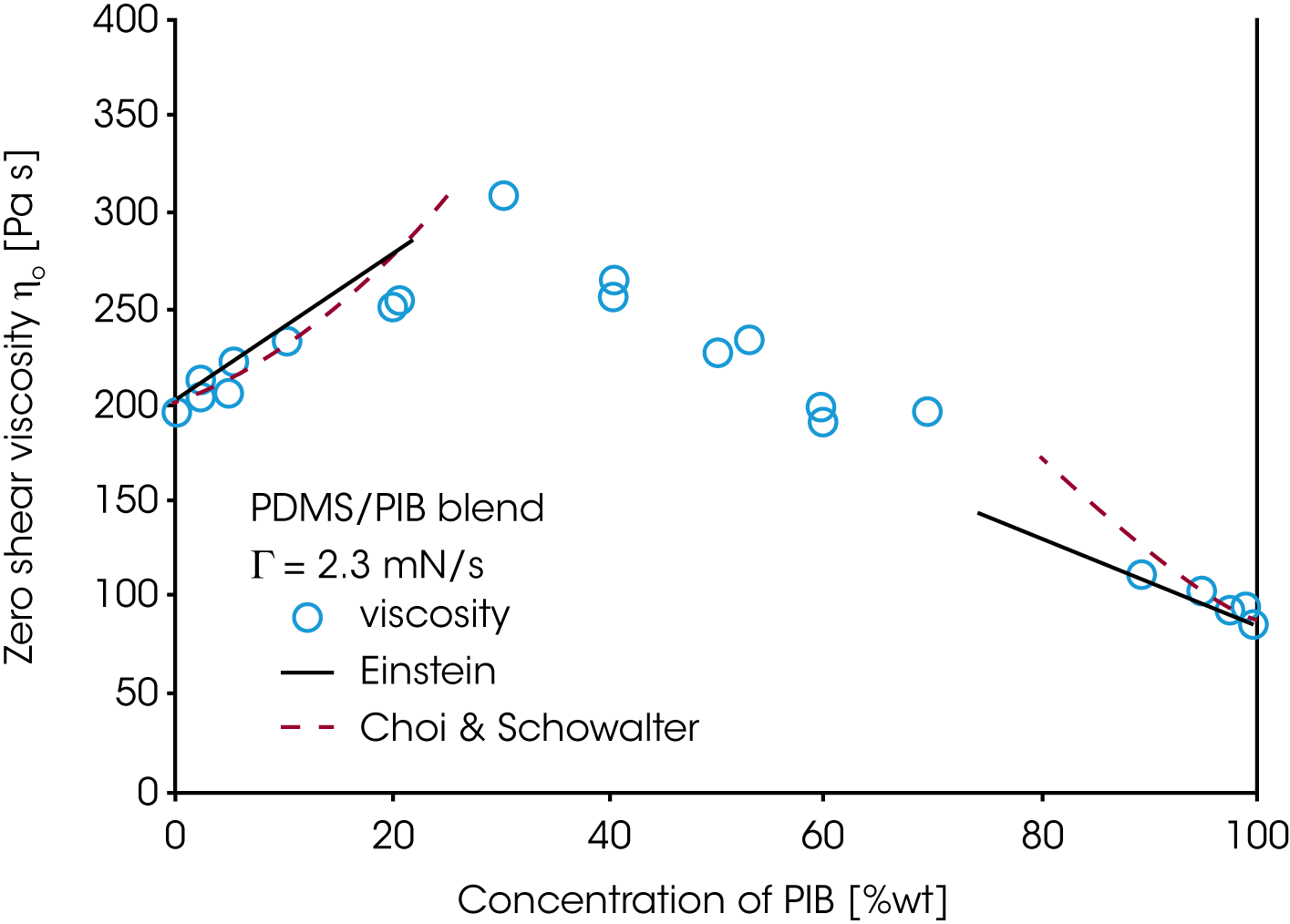
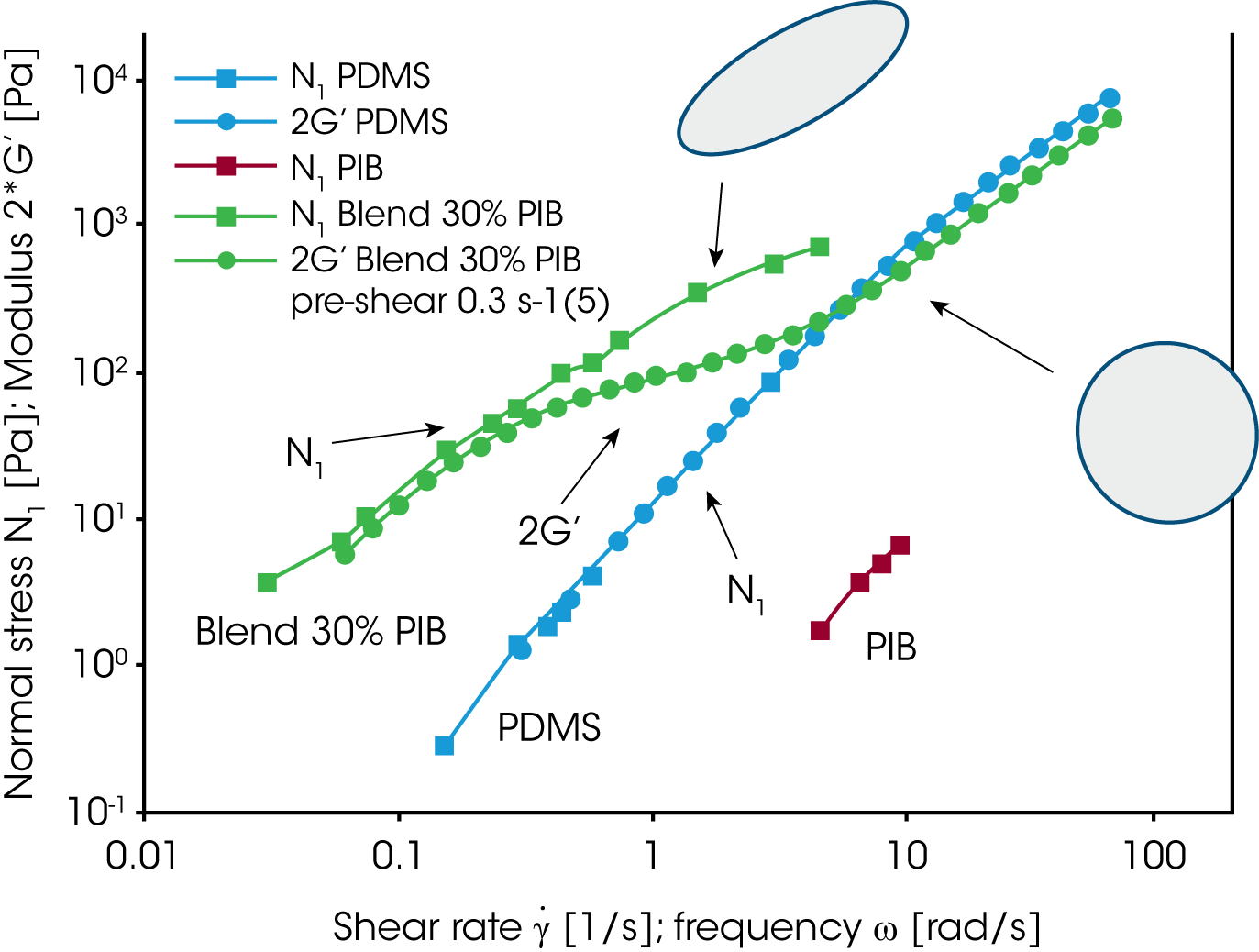
Die wichtigste Erkenntnis dieser Untersuchungen ist die, daß das rheologische Verhalten sehr stark durch die Morphologie geprägt wird und die Morphologie wiederum über die Strömungsbedingungen eingestellt werden kann. Die Folge ist, daß Mischungsgestze für nicht mischbare Polymersysteme sehr komplex werden. Für eine PDMS/PIB Mischung ist die Nullviskosität als Funktion des Mischungsverhältnisses in Bild 17 dargestellt. Nur bei kleinem Volumenanteil der dispergierten Phase kann das Emulsionsgesetz von Choi und Schowalter den Verlauf beschreiben /11/. Bei mittleren Mischungsverhältnissen sind zwei kontinuierliche Phasen vorhanden, die Morphologie bestimmt das rheologische Verhalten der Mischung und die bestehenden Mischungsgesetze gelten nicht mehr. In Abbildung 18 sind die Erkenntnisse für die PDMS/PIB Mischung zusammengestellt. Die erste Normalspannungsdifferenz N1 und der zweifache Wert des Speichermoduks G’ sind gegen die Scherrate bzw. die Frequenz aufgetragen, wobei dg/dt=ω. Bei kleiner Frequenz oder kleiner Scherrate überlagern sich die Daten aus der oszillatorischen und der zeitabhängigen Messung für die Elastizität (2G‘ and N1) der untersuchten Mischung.
Zu beachten ist, daß die Elastizitätswerte der reinen Komponenten wesentlich niedriger sind als die der Mischung. Bei kleiner Scherrate stört das Strömungsfeld im zeitabhängigen Versuch die Morphologie nur wenig und die großen Tropfen behalten weitgehend ihre sphärische Form bei. Mit zunehmender Rate werden diese deformiert. Wegen der gespeicherten Energie in der Grenzfläche bleibt die Normalspannungsdifferenz auf hohem Niveau bis die Tropfen bei sehr hohen Scherraten aufbrechen. Im Oszillationsversuch spricht die Phasenrelaxation nur auf die langsamen Frequenzen an. Mit zunehmender Frequenz werden nur noch die Relaxationsbeiträge der Ketten und Kettensegment erfasst und der Modul erreicht einen Wert der leicht unterhalb dem der reinen kontinuierlichen Phase liegt. Dieses Resultat ergibt sich aus einem leichten Verdünnungseffekt der dispersen Phase.
SCHLUSSFOLGERUNG
Mischungsregel sind wichtig um das Verhalten von mehrkomponenten Polymersystemen vorherzusagen. Das erweiterte Mischungsgesetz von Tsenoglou und Des Cloizeaux wird heute eingesetzt um die Molekulargewichtsverteilung von homologen Polymeren zu bestimmen. Das rheologische Verhalten von heterogenen Polymermischungen ist wesentlich schwierigher zu beschreiben. Neuere Konzepte und Ideen bei der Erstellung von Mischungsregeln haben das Verständnis heterogener, mischbarer Polymersysteme verbessert. Bei nicht mischbaren Polymersystemen dominiert die Morphologie weitgehend das rheologische Verhalten. Die Rheologie dieser Systeme hängt weiterhin sehr stark von der mechanischen Vorgeschichte ab und kann heute nicht befriedigend vorhergesagt werden.
REFERENZEN
- W.M. Prest Jr. Polymer J. 4, 2 (1973), 163
- C. Tsenoglou, New Trends in Physics and Physical Chemistry of Polymers, 375 (1989)
- J.C. Haley, et al. Macromolecules 36, 6142 (2003)
- J. Des Cloizeaux, Macromolecules 23, 3992 (1990)
- W.H. Tuminello presented SOR, Oct 1999
- T.P. Lodge, T.C.McLeish, Macromolecules 33, 5378 (2000)
- R. J. Composto, E. J. Kramer, and D. M. White, Macromolecules 25, 4167 (1992)
- S. Wu, J.Polym.Sci.Part B Polym.Phys. 25, 2511 (1987)
- C. Friedrich, et al. J.Rheol. 93, 1411 (1995)
- A. Einstein, A. Ann Phys. 19, 289 (1906), 24, 591 (1911)
- S.J. Choi, W.R. Schowalter Phys.Fluids 18, 420 (1975)(1975)
- Gramespacher et al. J.Rheol. 36(6) 1127 (1992)
- Vinckier et al. J.Rheol. 42(3), 705 (1997)
- J.F. Palierne, Rheol. Acta 29, 204 (1990)
- D.Graebling et al. European Polymer Journal, 30(3), 301 (1994)
- Vinckier et al. J.Rheol. 40(4), 613 (1996)
Acknowledgement
Click here to download the printable version of this application note.

