Characterizing Binding Interactions by ITC

Keywords: Isothermal Titration Calorimetry, binding, thermodynamics, assay, biomolecules

MC173

Introduction

All biochemical reactions involve recognition, binding and the formation of non-covalent complexes. Since the characterization of binding events is central to understanding any physiological process at the molecular level, biochemical and biomedical research requires methodologies for precisely analyzing binding reactions. Isothermal titration calorimetry (ITC) is rapidly becoming the method of choice for measuring intermolecular interactions, catalysis and binding equilibria, all with exquisite sensitivity. Both low affinity interactions such as some protein-protein interactions, and high affinity interactions such as protein-cofactor and enzymesubstrate binding, can be quickly and accurately characterized using nanomoles of native (underivatized) sample. For a general description of the principles behind ITC and the types of biological problems that can be addressed, please see TA Instruments’ Overview Note entitled “Life Science Applications of ITC.”

This Application Note surveys the utility of ITC for the analysis of noncatalytic macromolecular binding; an accompanying application note explains how ITC can be used to determine enzyme kinetic parameters.

Figure 1: ITC allows the rapid and accurate assessment of binding reactions, without the need to develop new assay protocols for each biomolecule or ligand. The stoichiometry of binding, and the association constant, enthalpy and entropy of the reaction can all be directly determined using just nanomoles of material. Note: ITC can characterize a binding reaction in about one hour.
Figure 1: ITC allows the rapid and accurate assessment of binding reactions, without the need to develop new assay protocols for each biomolecule or ligand. The stoichiometry of binding, and the association constant, enthalpy and entropy of the reaction can all be directly determined using just nanomoles of material. Note: ITC can characterize a binding reaction in about one hour.

Binding is Driven by Thermodynamics

Since all binding events are accompanied by the evolution or absorption of heat (a change in enthalpy, ΔH), a full thermodynamic characterizationof the binding reaction provides fundamental information about the molecular interactions driving the binding process. If the reaction being studied is, for example, the binding of a drug candidate to a mutant protein (co-expressed with native protein due to a genetic disorder), this thermodynamic information could suggest alterations to the chemical structure of the drug which would improve molecular interactions at the drug-protein interface, increased specificity for the mutant protein, heightened binding and enhanced efficacy of the drug. Although there are many techniques for studying binding reactions, all but one require that enthalpy be calculated from measurements, which introduces a degree of inaccuracy in the value of ΔH. Calorimetry is unique: at constant temperature and pressure, ITC directly measures the enthalpy of a binding reaction. A solution of one component (for example, a ligand such as a drug candidate) is titrated into a dilute solution of the second component (e.g., a mutant protein). At each injection of ligand into the sample,an equilibrium of free and bound ligand is established, and heat is released (exothermic) or absorbed (endothermic). At the end of the titration, all the binding sites in the sample are occupied and the observed association constant (Ka) can be calculated (Wiseman et al., 1989). Since temperature (T) is held constant throughout, the free energy (ΔG) of the binding reaction can be determined by:

MC173_Eq 01

lTC directly measures ΔH, so the change in entropy (ΔS) can be determined by:

MC173_Eq 02

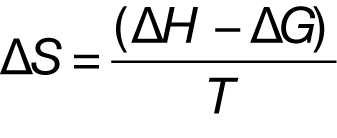
Thus, several 1–2 hour automated ITC experiments, requiring just nanomoles of sample, provide the association constant, enthalpy andentropy of the binding reaction. In addition, knowing the concentrations of the two components (e.g., ligand and protein) allows the stoichiometry of the binding reaction to be determined (Wiseman et al., 1989; O’Brien et al., 2001). Finally, if the titration is conducted at (at least) two temperatures, the change in constant pressure heat capacity (ΔCp) can be determined by:

MC173_Eq 03

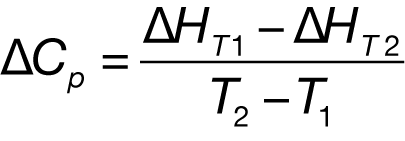
where T1 and T2 are the two temperatures at which the ITC experiments were conducted. Note that ΔCp may need to be corrected for coupled equilibra resulting from changes in hydration upon complex formation (Privalov and Privalov, 2000).

Quantification of these thermodynamic parameters reveals the physical processes involved in the binding reaction. A spontaneous binding process must have a negative ΔG, and ΔG will become increasingly negative as binding becomes tighter. As seen above, free energy changes have both an enthalpic and entropic component.

When two molecules interact noncovalently, they do so primarily through surface hydrophobic patches (unless binding triggers partialunfolding of a molecule such as a protein, thus exposing portions of the hydrophobic core). Binding specificity is provided by the precise pairing of hydrogen bond donors and acceptors, electrostatic interactions, dipole interactions, etc. If two molecules bind, they must display greater affinity for each other than they do for the solvent, as otherwise no binding would occur.

The enthalpic contribution to binding is primarily due to an increased number of hydrogen bonds with optimal (linear) donor-acceptor geometry and distance at the ligand-target interface, and to more favorable van der Waals interactions between the two interacting molecules; the hydrophilicity of the system will determine how important electrostatic, polar and dipolar interactions will be in driving the reaction. The entropic contribution has two primary components: conformational changes such as folding or unfolding of the macromolecules, and the release of bound solvent as hydrophobic groups interact. The large number of ordered water molecules released into the bulk solvent when the hydrophobic surfaces of the ligand and target interact provides the main driving force for hydrophobic interactions. This driving force is sufficient to compensate for the unfavorable conformational entropy of the macromolecule and ligand caused by decreased conformational and rotational freedom following binding. In addition to the entropic effect, burial of surface area also affects the heat capacity of the sample, since water molecules ordered at hydrophobic surfaces have a different heat capacity from that of water that has been released into the bulk solvent following binding.

Practical Implications

It is clear that many linked equilibria contribute to the overall heat effect, so as a stand-alone technique calorimetry provides global, rather than atomic-level, information about binding interactions. There are, however, two approaches for obtaining insights into the primary chemical and structural determinants driving an interaction. One is the systematic variation of the sample’s protonation environment: the location of a protonation event can often be established by repeating an ITC experiment either at several pHs, or at a single pH but using two buffers with different enthalpies of ionization (Gomez and Freire,1995; Baker and Murphy,1996). The second approach is to couple the thermodynamic data from ITC experiments with atomic-level (X-ray or NMR) structural data (Andujar-Sanchez et al., 2005; Hung et al., 2005; Wylie et al., 2005). This methodology is having a profound effect on the pharmaceutical industry. Prior to the widespread availability of ITC, it was difficult to correlate thermodynamic data with structural data: in the absence of a thermodynamic understanding of drugtarget interactions, affinities and specificities of drug candidates would be optimized in silico, but when synthesized and tested, the affinities of these compounds were often very different from what had been predicted. Since drug design was often guided only by predictions of the ΔG of an interaction, enthalpic contributions were frequently ignored, leading to disappointing laboratory results. The emergence of ITC as a front-line methodology in the drug development process is rectifying this problem. As totally automated ITC instruments with increased sensitivity and highthroughput capabilities become established in pharmaceutical screening laboratories, compounds with greater thermodynamic diversity will be used as starting points for improved drug design (Ladbury 2001; Holdgate 2001). Ultimately it may be possible to correlate structural detail with the thermodynamics of complex formation, making it possible to accurately predict binding events from thermodynamic first principles (Cliff and Ladbury, 2003; Luque and Freire, 2002). In addition, combining ITC information with data from other techniques (e.g., surface plasmon resonance, acoustic biosensors) will permit a total interrogation of the events occurring at the binding site; achieving this level of understanding will significantly impact such diverse fields as drug discovery, diagnosis, drug delivery and environmental monitoring (Cooper, 2003).

Practical Applications

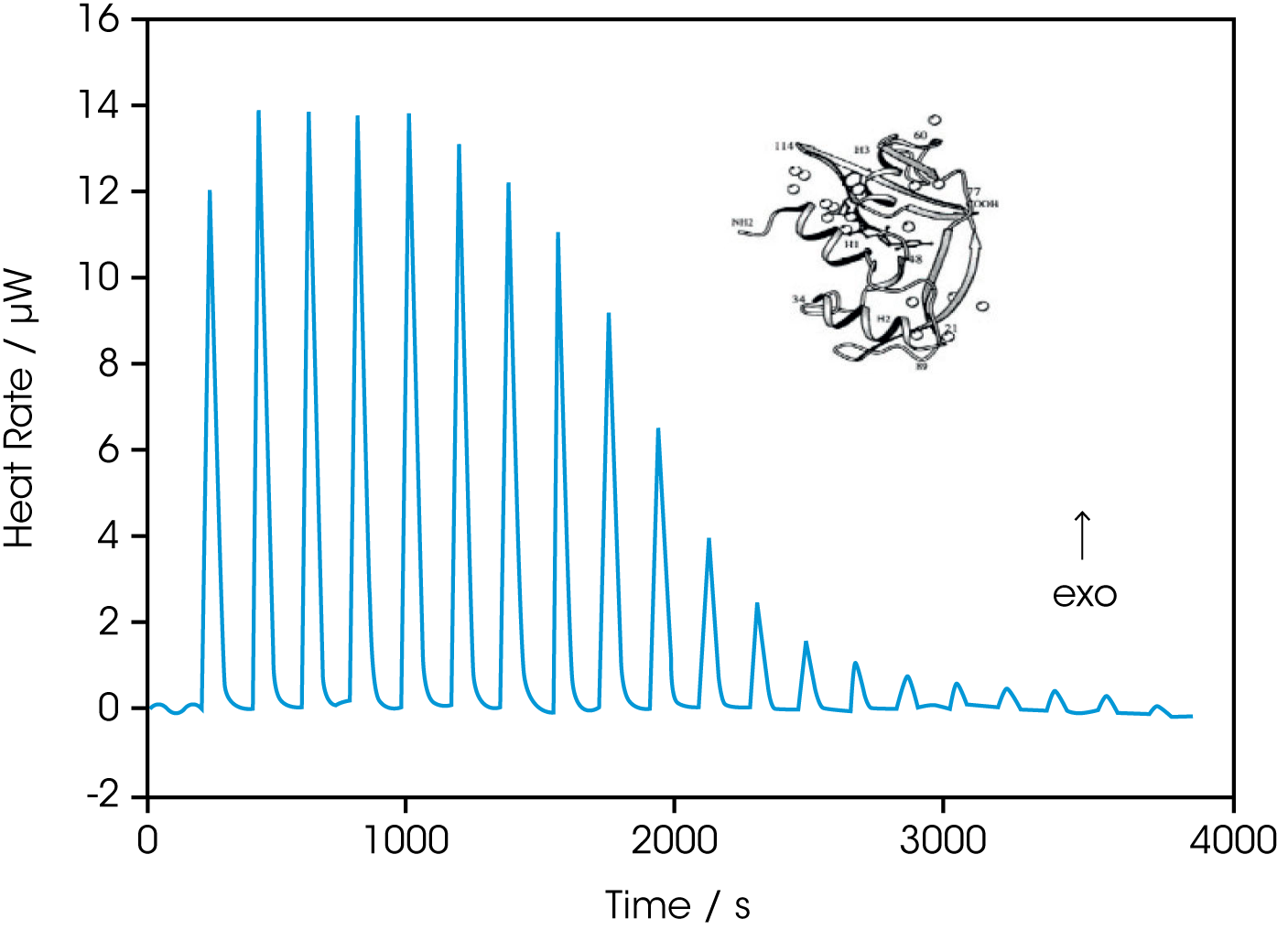
The design and analysis of an ITC experiment is illustrated by the titration of RNase A by the inhibitor cytidine monophosphate (2’CMP). Figure 2a depicts the signal produced by the sequence of injections, and Figure 2b shows the data after integration of each injection peak. The sigmoidal shape of Figure 2b, with numerous data points throughout the curved rise portion of the plot, facilitates estimation of the midpoint of the transition, and thus the stoichiometry of the binding reaction (in this case, 1:1). Ka and ΔH are calculated by iterative approximation. A value for Ka is initially estimated, then the concentration of bound complex is calculated for each injection. In combination with the measured heat, these values are used to determine the average of ΔH. The ΔH and the calculated concentration are then used to determine an expected heat per injection, and the error square sum between the measured and expected heat for each peak is calculated. The value of Ka is then adjusted and the process repeated until a minimum error square sum is obtained. These calculations are described in detail in Eatough et al. (1985), and are performed automatically with the “Bindworks” software supplied with CSC ITC instruments.

Figure 2: RNase A titrated with 2’-CMP in a TA Instruments ITC. RNase A was dialyzed (2 × 72 h, 4 °C) against 15 mM potassium acetate buffer, pH 5.5, then the concentration of the protein was adjusted to 80 μM. Ligand (1.58 mM 2’-CMP) was prepared using the final dialysis buffer. RNase A was loaded into the 7.0 mL sample cell and 2’-CMP was loaded into the 100 μL syringe. Twenty, 5 μL aliquots of ligand were titrated into the protein while the temperature of the system was maintained at 25°C. Figure 2a: The signal (heat) produced following each addition of inhibitor. Figure 2b: Integration of the heats over the time course of the experiment; the μJ in each peak are plotted against the mole ratio of titrant (inhibitor) to titrate (protein). ‘Exo’ depicts the sign convention for an exothermic reaction. Ka of 2’-CMP binding: 1 × 106 M-1. Enthalpy of binding: -65 KJ mol-1.
Figure 2: RNase A titrated with 2’-CMP in a TA Instruments ITC. RNase A was dialyzed (2 × 72 h, 4 °C) against 15 mM potassium acetate buffer, pH 5.5, then the concentration of the protein was adjusted to 80 μM. Ligand (1.58 mM 2’-CMP) was prepared using the final dialysis buffer. RNase A was loaded into the 7.0 mL sample cell and 2’-CMP was loaded into the 100 μL syringe. Twenty, 5 μL aliquots of ligand were titrated into the protein while the temperature of the system was maintained at 25°C. Figure 2a: The signal (heat) produced following each addition of inhibitor. Figure 2b: Integration of the heats over the time course of the experiment; the μJ in each peak are plotted against the mole ratio of titrant (inhibitor) to titrate (protein). ‘Exo’ depicts the sign convention for an exothermic reaction. Ka of 2’-CMP binding: 1 × 106 M-1. Enthalpy of binding: -65 KJ mol-1.

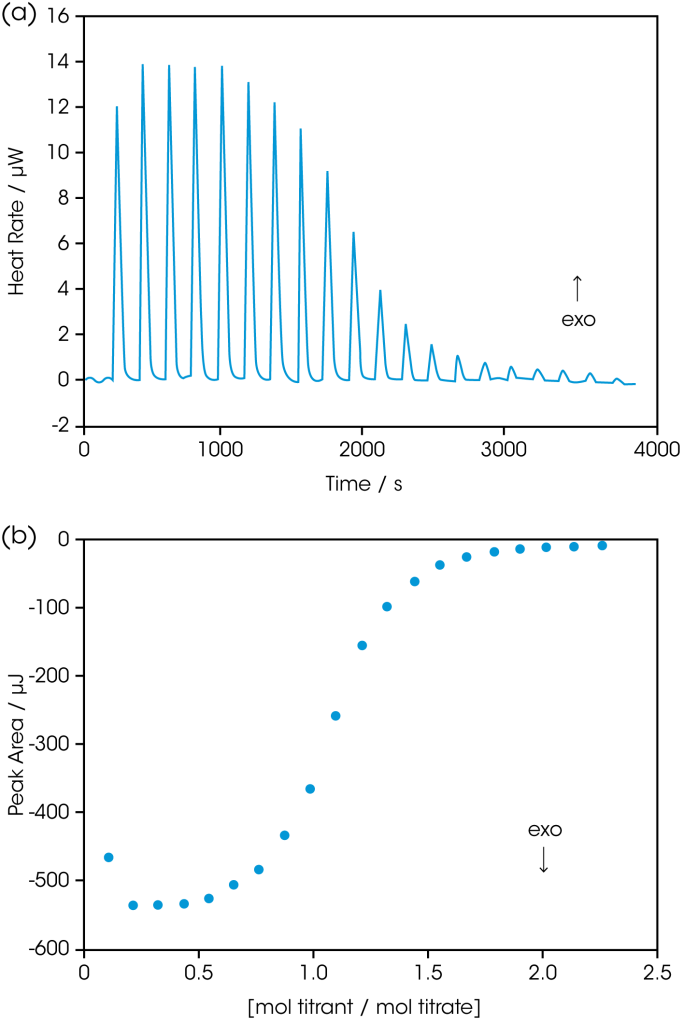
Ligand and macromolecule concentrations for an experiment can be chosen to optimize the measurement of interest. For example, if knowledge of ΔH is of primary concern, experiments should be performed under conditions of total association at partial saturation (high macromolecule concentration, resulting in complete binding of the ligand at the beginning of the titration) (Holdgate, 2001). If, as in the example above, the values of Ka, ΔH and n (stoichiometry) are all of interest,they can often be calculated from a single experiment as long as the concentration of both macromolecule and ligand are accurately known (O’Brien et al., 2001) and chosen so that:

MC173_Eq 04

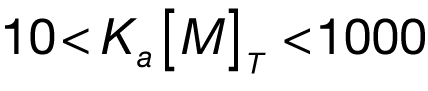
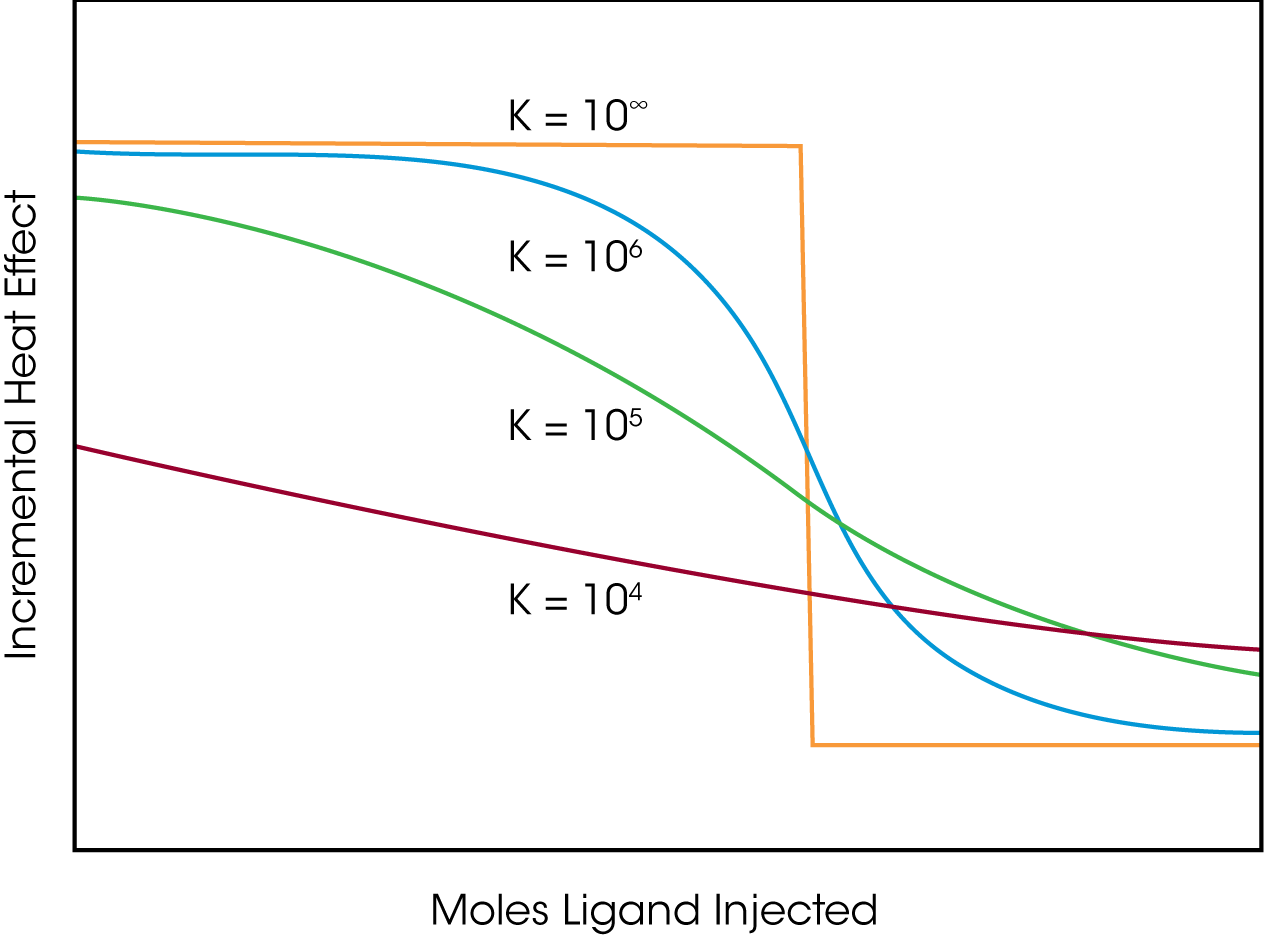
where [M]T is the total concentration of macromolecule in the sample cell titrated by ligand (Wiseman et al.,1989). If concentrations are not within this range, the curvature of the titration plot can be so low as to be almost linear, or so high as to produce a step-like profile; these scenarios are depicted in Figure 3.

Typically, macromolecule concentrations in the order of 10–100 μM are used, permitting Ka values in the range 102–109 M-1 to be accurately estimated. High protein and ligand concentrations have generally been used to determine affinities at the low end of this range, and low concentrations have been used to measure tight binding constants. Although highly concentrated solutions often experience solubility and aggregation problems, these can generally be overcome by using cosolvents, or if solubility of the ligand is the limiting factor, by conducting the titration in reverse (i.e., ligand in the sample cell, protein in the syringe) (Holdgate, 2001). Alternatively, continuous isothermal titration calorimetry, in which binding between a ligand and receptor molecule is studied by slowly and continuously titrating one reactant into the other over a period of 15–20 minutes, allows millimolar to micromolar (or tighter) binding to be quickly determined. Continuous titration experiments do not require any hardware modifications to the TA Instruments ITC instrument. Please see the application note entitled “Characterizing binding using continuous isothermal titration calorimetry” for a full description of this technique.

Competitive binding is yet another approach that can be used to measure very weak or very tight association constants (Khalifah et al., 1993; Zhang and Zhang,1998; Valazquez Campoy and Freire, 2005). In a competition experiment, two ligands with different affinities compete for the same binding site on a macromolecule. In a typical experiment to measure the Ka of a weaklybinding ligand, for example, approximately 50% of the binding sites would initially be occupied by the weak binder. Using lTC, the binding sites would then be incrementally filled by a ligand with a stronger affinity for the same site, displacing the weaker ligand. The process would be continued until all the binding sites were saturated with the strongly binding ligand. The extent to which the second ligand displaced the first will be dependant on the relative affinities and concentrations of the competing compounds. By knowing the Ka of the stronglybinding ligand, the Ka of the weak ligand (which has such a low binding constant that it cannot be accurately measured by direct ITC) can be calculated, without the need to resort to the high concentrations otherwise required (Figure 3). Competitive experiments can also be used to measure the Ka of very stronglybinding ligands (Valazquez Campoy and Freire, 2005).

Figure 3: The effect of binding affinity on the shape of the titration curve for a reaction with 1:1 stoichiometry. In these simulations, reactant concentrations and ΔH were held constant while Ka was varied. Low affinity reactions give an essentially straight line, while high affinity reactions give a rectangular curve at the reactant concentrations chosen. In order to be able to estimate Ka accurately, the product of the macromolecule concentration (in mol L-1 and the association constant should be between 10 and 1000.
Figure 3: The effect of binding affinity on the shape of the titration curve for a reaction with 1:1 stoichiometry. In these simulations, reactant concentrations and ΔH were held constant while Ka was varied. Low affinity reactions give an essentially straight line, while high affinity reactions give a rectangular curve at the reactant concentrations chosen. In order to be able to estimate Ka accurately, the product of the macromolecule concentration (in mol L-1 and the association constant should be between 10 and 1000.

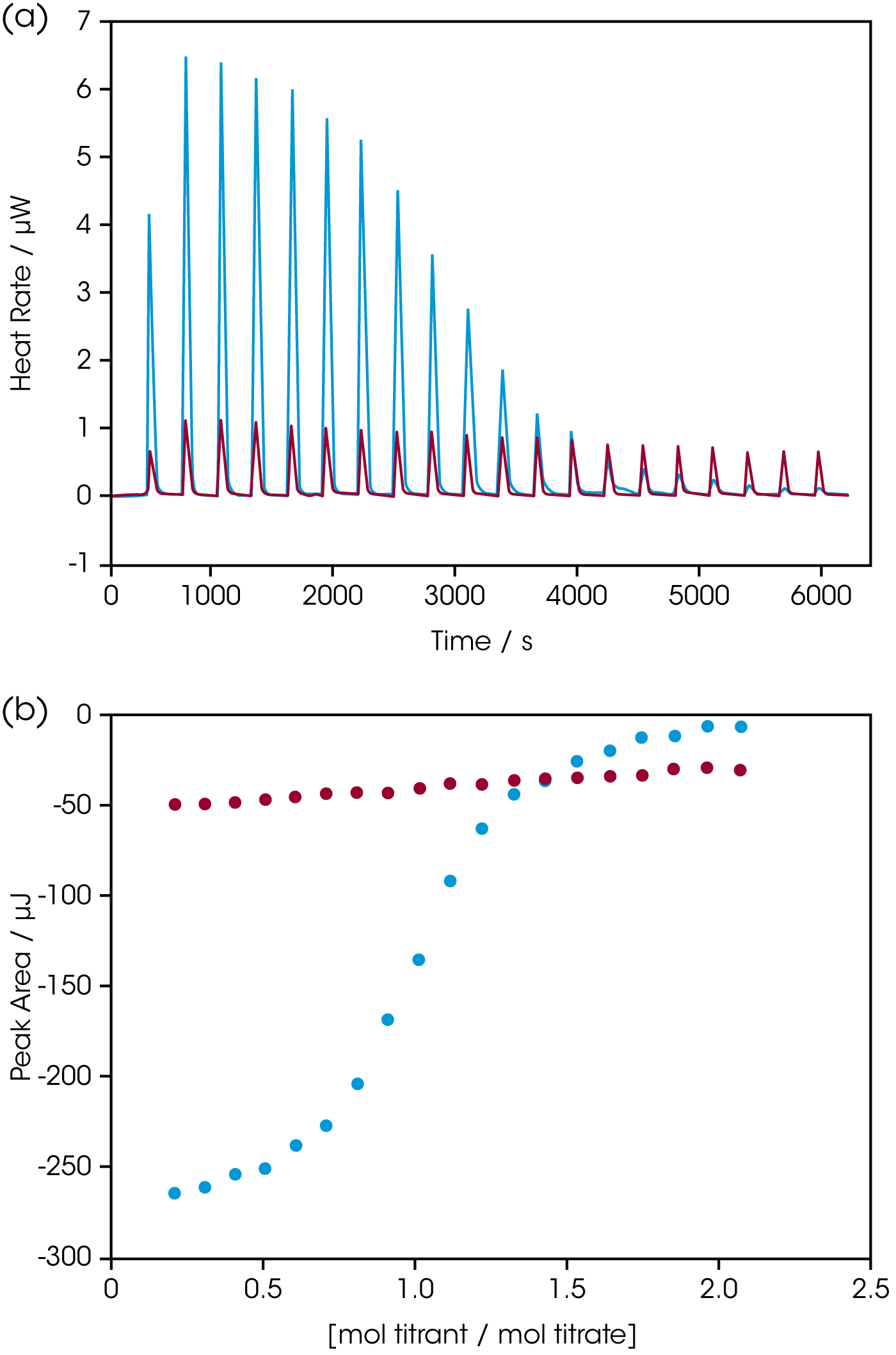
An application of the competitive binding approach for determining the Ka of a weakly-binding ligand is presented in Figure 4. The single binding site of RNase A is strongly inhibited by 2′-CMP (Figure 1), but so weakly inhibited by 5′-CMP that the affinity of 5′-CMP can only be roughly estimated at the concentrations used for this experiment (Figure 4). However, by introducing 2′-CMP as a competitor of 5′-CMP, both the Ka and enthalpy of binding of 5′-CMP to RNase A can be calculated (3100 M-1 and -47 kJ/mol, respectively; Figure 4). Holdgate (2001) and Sigurskjold (2000) present excellent reviews of the theory and application of competitive binding for ITC experiments. Valuable discussions of how to design and optimize ITC experiments, and approaches to analyzing the data, have been written by Leavitt and Freire (2001), Velazquez Campoy and Freire (2005) and Tellinghuisen (2005); an overview of applications of calorimetry to the drug discovery process is presented in Weber and Salemme (2003).

Summary

ITC is rapidly becoming the method of choice for characterizing binding reactions. The approach is completely general:small molecules binding to proteins, DNA, RNA and polysaccharides can all be studied in an analogous manner, as can protein-protein, protein-nucleic acid and nucleic acid-nucleic acid interactions. The increasing prominence of ITC as a fundamental tool in biochemical and biomedical research is due to the accurate assessment of binding interactions that can be quickly obtained, without the need to develop new assay protocols for each biomolecule or ligand; in addition, its direct nature and high precision make it invaluable in validating the results of less rigorous, high throughput assay protocols.

Red: incremental titration of 5′-CMP into RNase (950 μL 70 μM RNase in the sample cell; 100 μL 1.3 mM 5′-CMP in the syringe titrated into the RNase solution in 20, 5 μL increments). All solutions were prepared in 0.15 mM acetate buffer, pH 5.5, and experiments were conducted at 25°C. Very low heat rates are obtained (top panel); integration of the heats over the time course of the experiment yields a line with little curvature (lower panel). Binding models fit to this data can only provide a rough estimate of the binding constant.

Blue: Incremental titration of 2′-CMP into RNase prebound with 5′-CMP (950 μL 70 μM RNase prebound with 0.32 μM 5′-CMP; 100 μL 1.3 mM 2’‑CMP in the syringe titrated into the RNase solution in 20, 5 μL increments. Solutions were prepared in the same buffer as above, experiment conducted at 25°C. The displacement titration yields significant heats of binding (top panel), providing a graph of integrated heats (bottom panel) that can be fit to the correct model (independent binding, stoichiometry of 1) using the NanoAnalyze software provided with the ITC. Knowing the binding constant for 2′-CMP (Figure 1) allows the binding constant of 5’‑CMP (3100 M-1) and the enthalpy of binding (-47 kJ/mol) to be accurately calculated, without having to resort to high concentrations of RNase. Both values are in agreement with previous measurements (Velazquez Campoy and Freire, 2005). Note that the displacement experiment yields heat rates and integrated heats approximately half that obtained by the titration of 2′-CMP alone into RNase (Figure 2).

Please refer to TA Instruments’ application note entitled “Characterizing protein/ligand binding by DSC” to see how DSC can augment lTC data by measuring very high binding affinities, and by measuring affinities in the presence of high concentrations of organic solvent.

Figure 4: Determining the binding constant of a very weaklybinding ligand using a TA Instruments calorimeter. RNase A binds both 2’-CMP and 5’-CMP in the same binding pocket, but shifting the hydroxyl group from the 2’ to the 5’ position significantly decreases the binding affinity of the ligand.
Figure 4: Determining the binding constant of a very weaklybinding ligand using a TA Instruments calorimeter. RNase A binds both 2’-CMP and 5’-CMP in the same binding pocket, but shifting the hydroxyl group from the 2’ to the 5’ position significantly decreases the binding affinity of the ligand.

References

(Preference has been given to current references. Citation does not imply that a paper is necessarily the original reference to a study.)

  1. Andujar-Sanchez, M. et al. (2005) Crystallographic and thermodynamic analysis of the binding of S-octylglutathione to the Tyr 7 to Phe mutant of glutathione S-transferase from Schistosoma japonicum. Biochemistry 44,1174-1183.
  2. Baker, B. M. and K. P. Murphy. (1996) Evaluation of linked protonation effects in protein binding using isothermal titration calorimetry. Biophys. J. 71, 2049-2055.
  3. Cliff, M. J. and J. E. Ladbury. (2003) A survey of the year 2002 literature on applications of isothermal titration calorimetry. J. Mol. Recognit.16,383-391.
  4. Cooper, M. A. (2003) Label-free screening of bio-molecular interactions. Anal. Bioanal. Chern.377,834-842.
  5. Eatough, D. J., E. A Lewis and L. D. Hansen. (1985) Determination of ΔHR and Keq values. p. 137-161. In K. Grime (Ed.) Analytical Solution Calorimetry. John Wiley and Sons.
  6. Gomez, J. and E. Freire. (1995) Thermodynamic mapping of the inhibitor site of the aspartic protease endothiapepsin. J. Mol. Biol. 252,337-350.
  7. Holdgate, G. A. (2001) Making cool drugs hot: isothermal titration calorimetry as a tool to study binding energetics. BioTechniques 31,164-184.
  8. Hung, K-W. et al. (2005) Solution structure of the ligand binding domain of the fibroblast growth factor receptor: role of heparin in the activation of the receptor. Biochemistry 44,15787-15798.
  9. Khalifah, R. G., F. Zhang, J. S. Parr and E.S.Rowe. (1993) Thermodynamics of binding of the CO2-competative inhibitor imidazole and related compounds to human carbonic anhydrase 1: an isothermal titration calorimetry approach to studying weak binding by displacement with strong inhibitors. Biochemistry 32, 3058-3066.
  10. Ladbury, J. E. (2001) Isothermal titration calorimetry: application to structure-based drug design. Thermochim. Acta 380, 209-215.
  11. Leavitt, S. and E. Freire. (2001) Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr. Opin. Struct. Bioi. 11,560-566.
  12. Luque, I. and E. Freire. (2002) Structural parameterization of the binding enthalpy of small ligands. Prot.- Struct. Funct. Genet. 49,181-190.
  13. O’Brien, R., J. E. Ladbury and B. Z. Chowdry. (2001) Isothermal titration calorimetry of biomolecules. p. 263-286. In S. E. Harding and B. Z. Chowdry (Eds.) Protein-Ligand Interactions: hydrodynamics and calorimetry. Oxford University Press, Oxford.
  14. Privalov, G. P. and P. L. Privalov. (2000) Problems and prospects in microcalorimetry of biological macromolecules. Meth. Enzymol. 323,31-62.
  15. Sigurskjold, B. W. (2000) Exact analysis of competition ligand binding by displacement isothermal titration calorimetry. Anal. Biochem. 277,260-266.
  16. Tellinghuisen, J. (2005) Optimizing experimental parameters in isothermal titration calorimetry. J. Phys. Chem. B 109,20027-20035.
  17. Valazquez Campoy, A. and E. Freire. (2005) lTC in the postgenomic era…? Priceless. Biophys. Chern. 115,115-124.
  18. Weber, P. C. and F. R. Salemme. (2003) Applications of calorimetric methods to drug discovery and the study of protein interactions. Curr. Opin. Struct. Bioi. 13, 115-121.
  19. Wiseman, T. ,S. Williston, J. F. Brants and L. N. Lin. (1989) Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 179,131-137.
  20. Wylie, G. P. et al. (2005) Prolylpeptide binding by the prokaryotic SH3-Iike domain to the diphtherial toxin repressor:a regulatory switch. Biochemistry 44,40-51.
  21. Zhang, Y-L and Z-Y Zhang. (1998) Low-affinity binding determined by titration calorimetry using a highaffinity coupling ligand: a thermodynamic study of ligand binding to protein tyrosine phosphatase 1B1. Anai. Biochem. 261,139-148.

Click here to download the printable version of this application note.

Contact us to learn more about our instrumentation and how it can benefit your research.