Keywords: Rheology, Cure, Gelation, Kinetics
RH103
Background
The gel point in a curing system can be used to monitor the progression of the curing reaction and to determine the kinetics of the gelation. The gel point can be determined via rheological methods so we can use a rheometer to measure the gelation kinetics. We use an epoxy system, measured on a Discovery Hybrid Rheometer, as an example in this note.
Experimental
The sample was a two-part commercial epoxy. The parts were mixed at room temperature and loaded immediately. Care was taken to avoid the formation of bubbles while mixing. It is important that no significant curing take place before loading the sample and starting the experiment. Samples that are mixed and stored should be stored at sufficiently low temperatures as to minimize curing before the measurement starts.
The sample was measured on aluminum 25 mm diameter disposable parallel plates. The initial gap was 1 mm with the instrument set to maintain 0 ± 0.1 N of axial force. A strain of 0.05% (min torque of 5 μNm) and frequency of 1 Hz was used for all measurements. The environmental test chamber was used to preheat the geometry before loading and control temperature during the tests. Materials were loaded and trimmed quickly. Data collection started as soon as the sample was loaded, trimmed, and the chamber doors were closed.
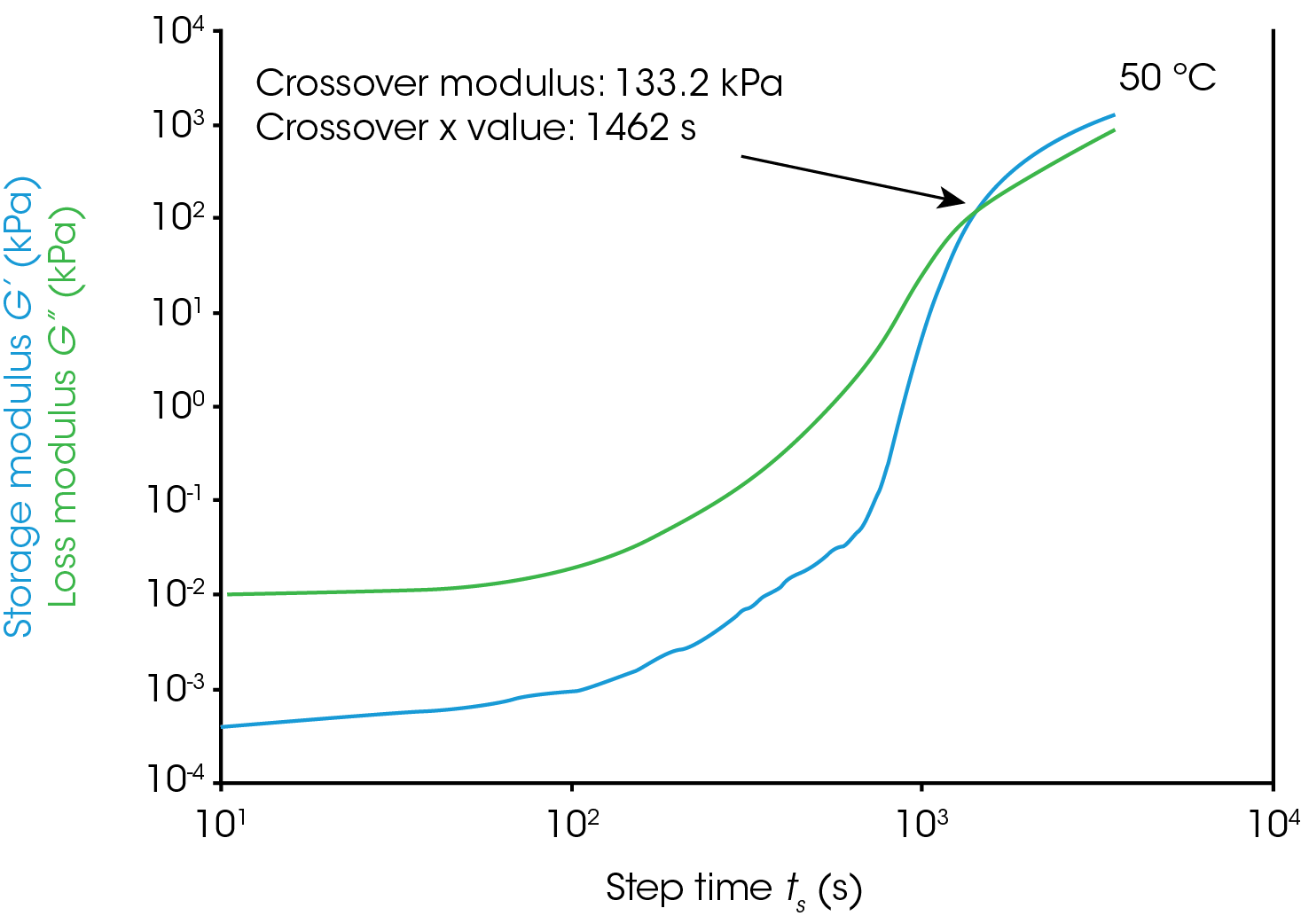
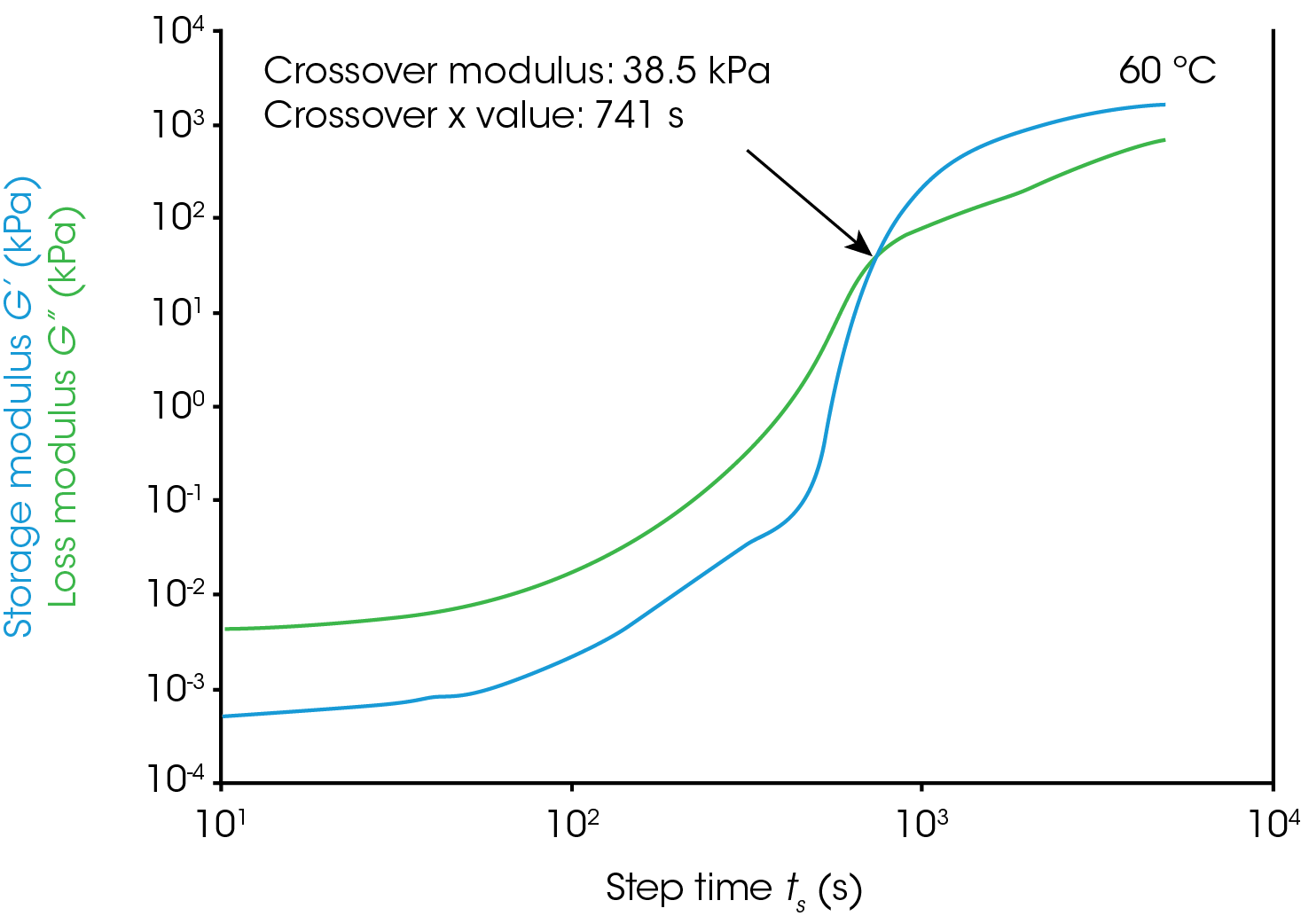
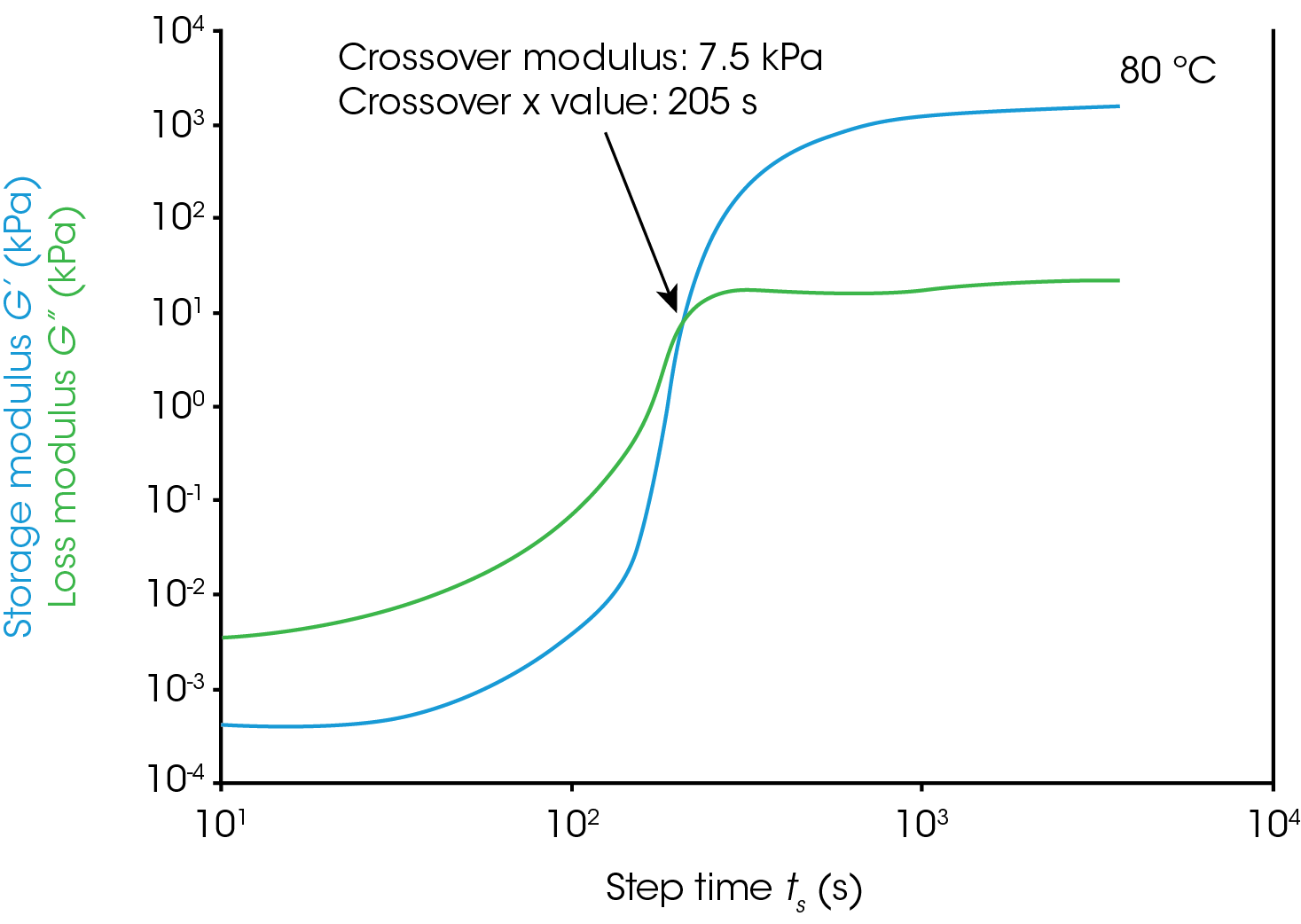
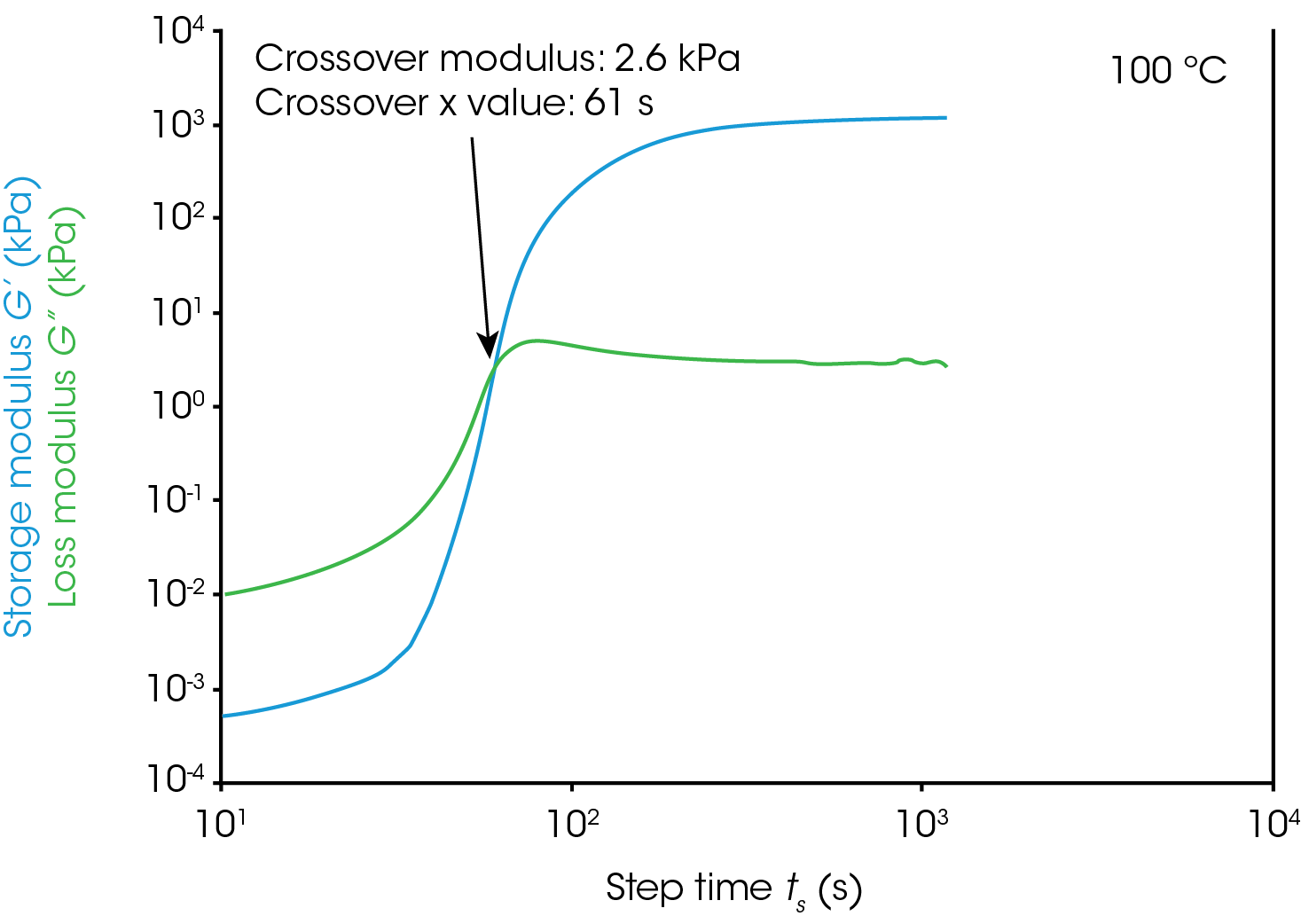
Gel Point
Figure 1 shows rheological data from an isothermal test, performed at 4 different temperatures. In this note, we will denote the point where the storage modulus crosses over the loss modulus as the gel time. This is also the point at which tan(δ) is equal to 1. The modulus crossover is a convenient point to use in systems where the loss modulus starts higher than the storage modulus and reverses as the material cures. The G’/G” crossover may not represent the “true” gel point of the system, since the crossover will be frequency dependent, but we will use it as a close approximation in this note. Winter et al [1] have proposed another rheological approach for determining the “true” gel point of a curing system. This method is particularly useful for instances where the storage modulus before the cure is higher than the loss modulus and there is no modulus crossover.
Gelation Kinetics
For this system, a simple analysis of gelation kinetics can be performed on the data shown in Figure 1 using the time to gelation at different temperatures. The four temperatures and four gel times can be used to determine the activation energy. We will use the following relation [2,3]
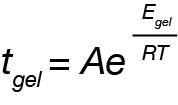
Which we can linearize to
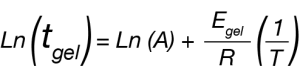

Where tgel is our approximated gel time, A is a constant, Egel is the gelation activation energy, R is the universal gas constant, and T is the temperature of the isothermal ramp. We use this relation and our approximated gel time to create the plot in Figure 2 and a linear fit to determine Egel/R as the slope of the line.
For the data in this note, we determine Egel to be 63.6 kJ/mol. This information, and the constant A, allow us to predict the approximate tgel for this system at any temperature. An example calculation is shown below for the tgel near room temperature (303 K): the sample would show a tgel of 7115 seconds (~around 2 hours). The factor A sets the time units of the relationship.
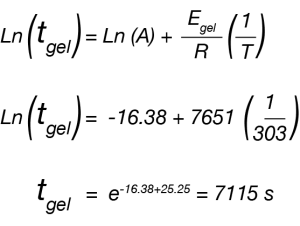
Conclusion
This note has demonstrated that the kinetics of gelation for a curing reaction can be estimated via rheological measurements to obtain useful results with predictive power. The approximate gel time of using the modulus crossover can be used in this epoxy system. Systems that are more elastic at the start of the test, such as a glass braid with epoxy on it or a highly filled system can use the true gel point from the Winter-Chambon criterion.
References
- H. Winter, F. Chambon, Analysis of Linear Viscoelasticity of a Crosslinking Polymer at the Gel Point, J. of Rheo, 1986, vol 30 p367
- Vlassopoulos D, Chira I, Loppinet B, et al. Gelation kinetics in elastomer/thermoset polymer blends. Rheol Acta 1998; vol 37, 614–623.
- M. Yang, D. Wang, N. Sun, C. Chen, X. Zhao, Rheological Behaviour and Cure Kinetic Studies of a Trifunctional Phenylethynyl-Terminated Imideoligomer, High Performance Polymers, 2015, vol 27, p449
Acknowledgement
This paper was written by Dr. Kevin Whitcomb, Applications Support Engineer at TA Instruments and Dr. Tianhong Terri Chen, Senior Applications Support Scientist at TA Instruments.
Click here to download the printable version of this application note.

