Keywords: modulated thermomechanical analysis, MTMA, battery separator, lithium ion battery, polypropylene
TA463
Abstract
Modulated thermomechanical analysis (MTMA) was performed on a polypropylene (PP) battery separator to gain further insight into the mechanism of the dimension change and coefficient of linear expansion (CLE or α). Dimension change measurements were made in the subambient range and at the determined shrinkage onset, deformation, and rupture temperatures. CLE was determined at selected temperature ranges up to the rupture temperature. In both the subambient and upper temperature ranges, the anisotropic nature of the film is observed by the significantly higher positive CLE in the transverse direction (TD) relative to the machine direction (MD). Contraction in the MD in the non-reversing dimension change is observed at approximately 80 °C which is eventually followed by rupture. The expansion in the reversing dimension change is positive up to the point of rupture in the MD. The non-reversing dimension change contributes more to the total dimension change than the both the MD and the TD throughout the entire temperature range. MTMA is an excellent tool for investigating the effects of processing by separating those effects from inherent thermal expansion properties.
Introduction
The safety mechanism of anisotropic battery separators like Celgard 2400® is the contraction of the film during overheating which collapses the porous structure effectively stopping the electrochemical reaction and shutting down the battery. The contraction results from relief of induced stresses imparted to the separator due to uniaxial stretching during the manufacturing process. Modulated TMA separates dimension change into reversing and non-reversing components which provides more insight into the dimension change mechanism which can aid in separator design.
In general, when materials are heated, they expand and when cooled they contract to their original dimensions. This type of expansion is reversible and the rate of length of change with respect to temperature is the CLE (Equation 1). If the material is heated and is subjected to a load, it may soften and flow (creep). This dimension change is not reversible as the sample will not return to its original dimensions simply by cooling. Similarly, if the material is softened by heating, stretched, and then cooled, residual stresses will be left in the sample. On subsequent heating the material will relax and shrink. This deformation is also non-reversible. In an isotropic material, the rate and extent of expansion is consistent in all directions contrasted with an anisotropic material where the expansion and rate are not consistent in all directions.
TMA measurement is a summation of all these effects unless the sample is isotropic and under no load. Separation of the temperature dependent reversing thermal expansion from the time and temperature dependent non-reversing expansion (or contraction) is possible utilizing MTMA. The total rate of dimension change as the summation of the temperature dependent reversing component and time and temperature non-reversing component is expressed in Equation 1.
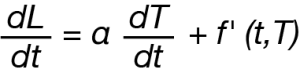
Where L is the sample length, α is CLE, and f’(t,T) is a function of time and temperature describing dimension changes due to applied load or relaxation of stresses [1].
MTMA superimposes a sinusoidal temperature heating rate on a linear heating rate or static heating (quasi isothermal). Fourier transformation of the oscillatory temperature forcing function and resultant response provides the deconvolution of these signals into reversing and non-reversing expansion components. An example of the modulated temperature and resultant rate of dimension change is shown in Figure 1 [2]. The total dimension change is the sum of the reversing and non-reversing dimension changes.
The calculations and experimental procedures for the standard TMA test for materials are documented in ASTM E 831 [3].
In a previous application note [4], TMA was used to characterize a uniaxially stretched PP battery separator (Celgard 2400) in both the machine (MD) and transverse (TD) directions. In this note, MTMA is used to gain further insights into the relative contributions to the dimension change and rate of dimension change of the reversing and non-reversing components.
![TA463_Fig.1 Figure 1. Modulated temperature and resultant modulated length from TA311 [2]](https://www.tainstruments.com/wp-content/uploads/TA463_Fig.1.png)
Experimental
The sample used was Celgard 2400 (PP) which was obtained commercially.
Table 1. MTMA Experimental Conditions
| Instrument | Discovery® 450 TMA |
| Sample Width | 2 mm |
| Sample Length | 13 mm |
| Sample Thickness | 25 μm |
| Applied Force | 0.02 N |
| Period | 300 s |
| Ramp Rate | 1 °C / min |
| Purge | N2 at 50 mL/min |
Results and Discussion
Subambient Temperature Range
The subambient (10 °C to -40 °C) dimension changes in the MD and TD are summarized in Table 2. The anisotropic nature of the separator is indicated by the significant difference in both the reversing expansion and non-reversing expansion in TD compared to MD. Most of the dimension change in both directions occurs in the non-reversing expansion which indicates that it is mainly due to the stretching process. It may also be useful to evaluate a sample of non-stretched film as a reference. The expansion characteristics in the subambient range are also important as the working temperature range for batteries may also include very low temperatures – such as batteries used to power automobiles.
Table 2. Dimension change in subambient range from 10 to -40 °C in MD and TD
| Instrument | MD | TD |
| Reversing (μm) | -2.95 | -23.86 |
| Non-Reversing (μm) | -5.51 | -37.91 |
| Total (μm) | -8.46 | -61.77 |
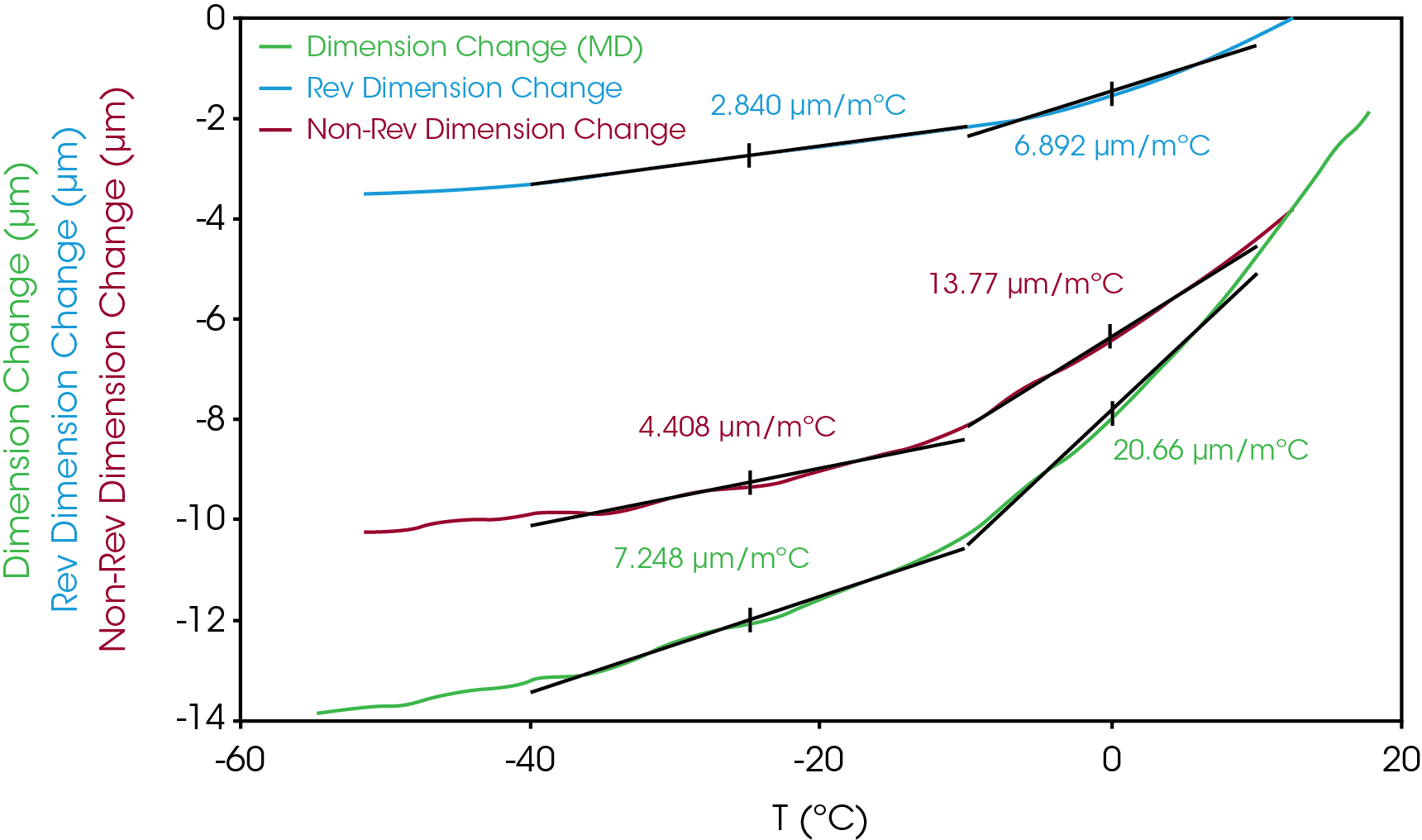
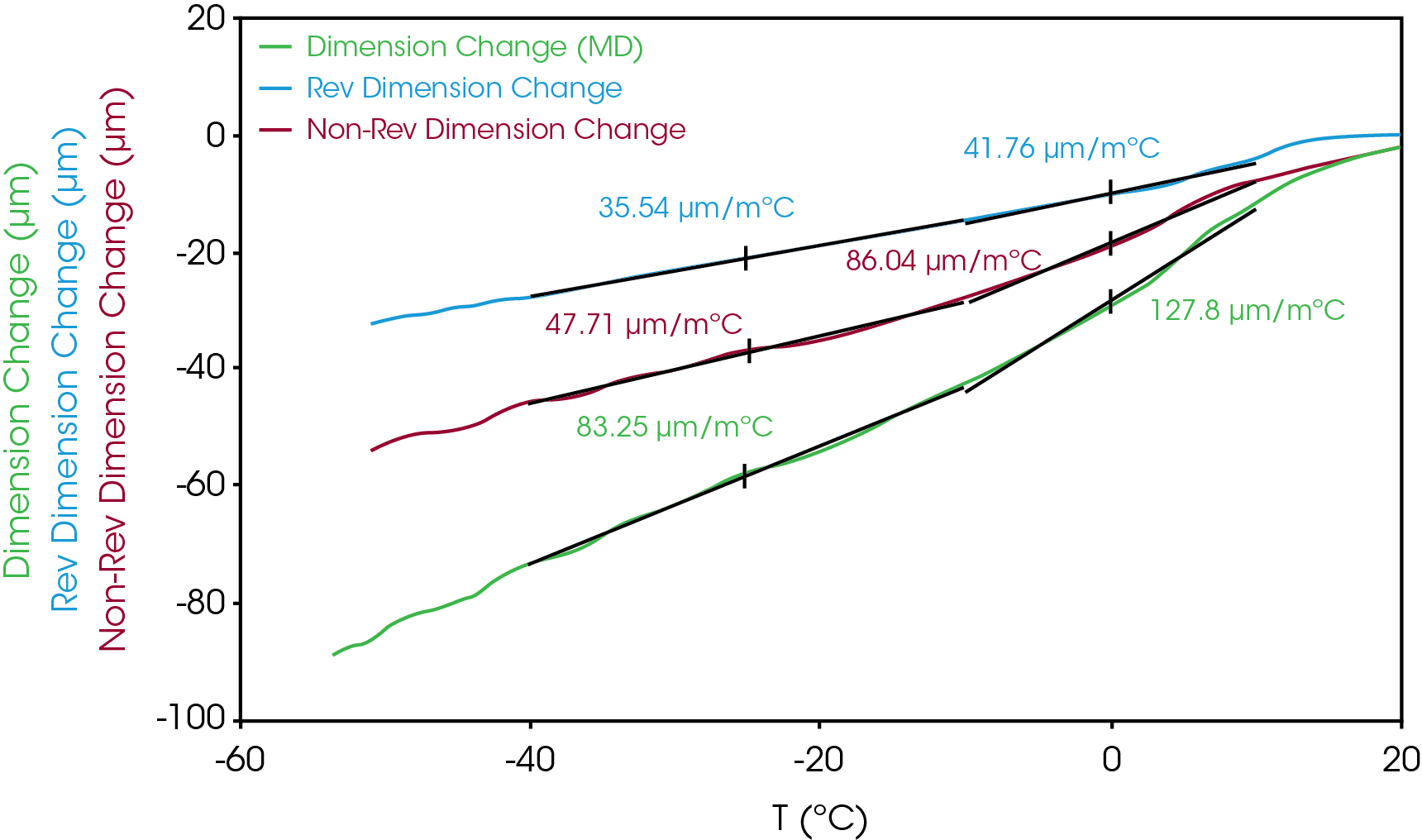
CLE values (α) in the subambient range are summarized in Table 3 and shown in Figure 2 and Figure 3. As expected, the values are significantly greater in the TD relative to the MD with the non-reversing greater than the reversing in both directions. The decrease in α at just below 0 °C is due to the PP glass transition.
Table 3. CLE (α) in MD and TD for subambient range from 10 to -40 °C (units in μm/m or ppm)
| Machine Direction | -10 to 10 °C | -10 to -40 °C |
| Reversing | 6.89 | 2.84 |
| Non-Reversing | 13.77 | 4.41 |
| Total | 20.66 | 7.25 |
| Transverse Direction | -10 to 10 °C | -10 to -40 °C |
| Reversing | 41.76 | 35.54 |
| Non-Reversing | 86.04 | 47.71 |
| Total | 127.8 | 83.25 |
Ambient to Upper Temperature Range
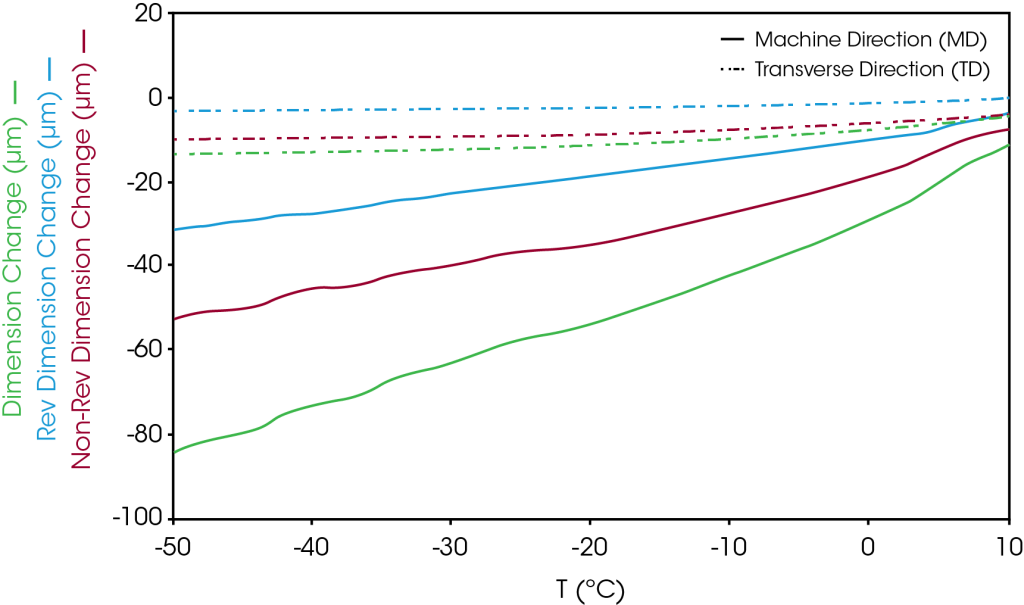
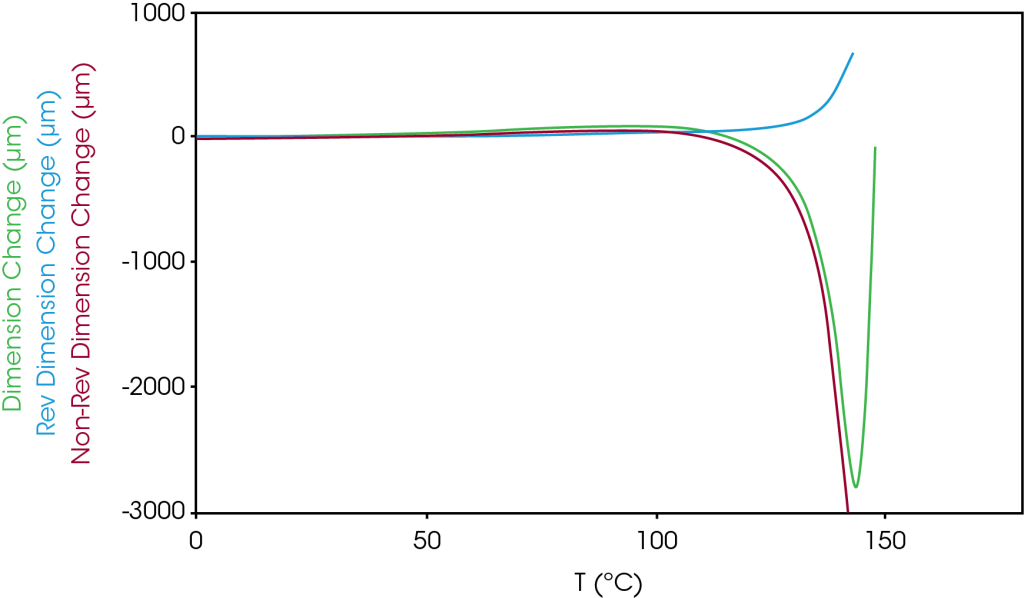
MTMA results in the MD from just below ambient to the rupture temperature are shown in Figure 4. The reversing dimension change (blue) is positive through the temperature range to rupture. The non-reversing dimension change (red) becomes negative (contracts) when the sample reaches a temperature that the stresses are relieved. The sum of the reversing and non-reversing dimension changes comprises the total dimension change (green). The MTMA experiment allows measurement of expansion and contraction simultaneously.
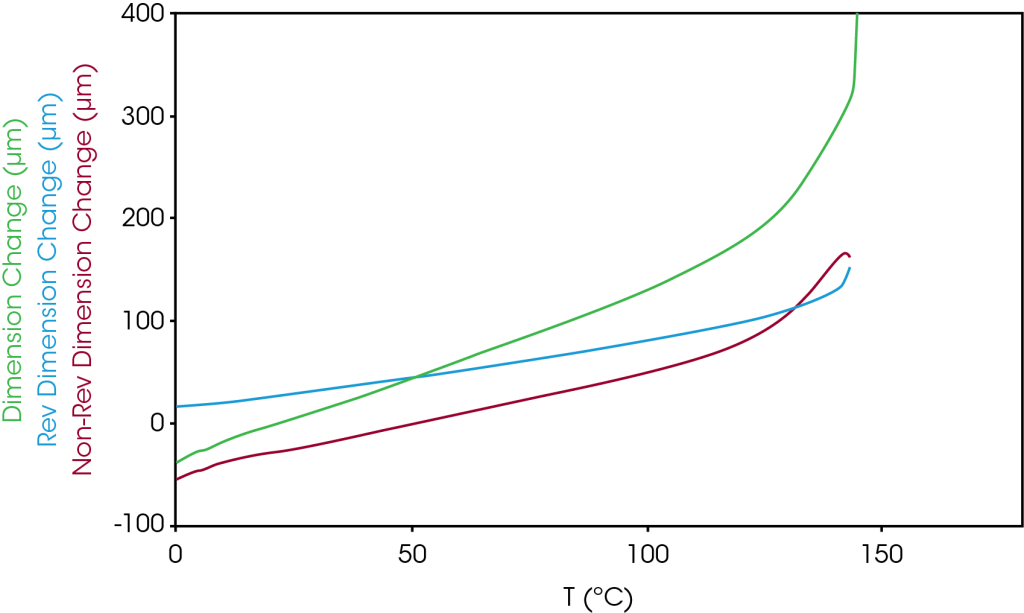
The MTMA results in the TD are shown in Figure 5. All dimension changes are positive – no contraction due to relieved stresses are observed.
The dimension change at the shrinkage onset temperature, the deformation temperature, the rupture temperature, and at 60 °C was determined. To obtain these temperatures, we used the dimension change signal in the MD utilizing the alternative method described in the previous application note [4]. Also included was the expansion at 60 °C chosen arbitrarily as an upper limit that a battery may experience under normal operation. The determined parameters and temperatures are shown in Table 4.
Table 4. Parameters from MTMA experiment – total dimension change in machine direction
| Parameter | Temperature °C |
| Shrinkage Onset | 100.0 |
| Deformation | 131.8 |
| Rupture | 143.7 |
Dimension changes separated into total, reversing, and non-reversing components for the MD are shown in Table 5. The non-reversing dimension change is the largest contributor to the overall dimension change in the MD. At the shrinkage onset, all the dimension change values are positive. At the deformation temperature, the non-reversing contributes a large contraction that is partially offset by the positive expansion in the reversing dimension change. At the rupture temperature, the reversing dimension change remains positive with the overall dimension change showing contraction.
Table 6 summarizes the dimension changes in the TD and just as in the MD, most of the contribution is from the non-reversing dimension change. At 60 °C and shrinkage onset, greater expansion is observed in the TD direction and is positive.
Table 5. MD dimension changes
| Parameter | Dimension Change (μm) | Reversing Dimension Change (μm) | Non-Reversing Dimension Change (μm) |
| Shrinkage Onset | 85.93 | 34.19 | 51.74 |
| Deformation | -483.7 | 131.4 | -615.1 |
| Rupture | -2728 | 674.6 | -3414 |
| 60 °C | 43.38 | 12.73 | 30.65 |
Table 6. TD dimension changes
| Parameter | Dimension Change (μm) | Reversing Dimension Change (μm) | Non-Reversing Dimension Change (μm) |
| Shrinkage Onset | 129.0 | 52.55 | 76.44 |
| Deformation | 225.9 | 85.12 | 140.7 |
| Rupture | 311.6 | 121.3 | 190.2 |
| 60 °C | 59.06 | 23.14 | 35.923 |
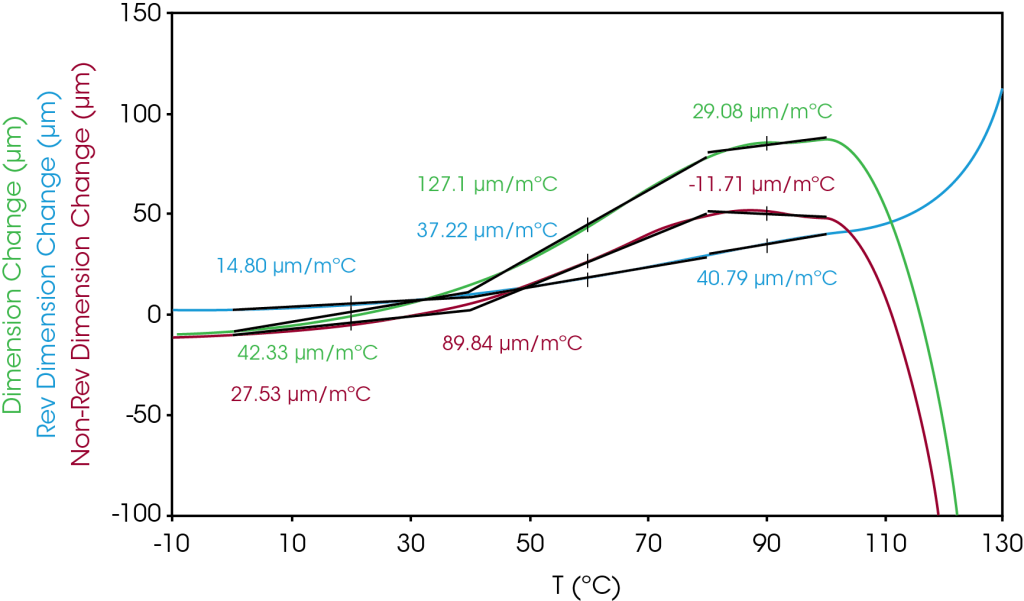
CLE values in the MD for selected temperature ranges up to the maximum positive expansion are shown in Figure 6 and Table 7 and for the TD in Figure 7 and Table 8. The CLE values in the TD are significantly higher than in the MD before shrinkage occurs.
The effect of the film stretching is the major factor in the expansion change indicated by the larger contribution of the non-reversing expansion to the total expansion.
Table 7. MD CLE values from Figure 6
| Temperature Range °C |
Total (ppm) | Reversing (ppm) | Non-Reversing (ppm) |
| 0 – 40 | 42.33 | 14.80 | 27.53 |
| 40 – 80 | 127.1 | 37.22 | 89.84 |
| 80 – 100 | 29.08 | 40.79 | -11.71 |
Table 8. TD CLE values from Figure 7
| Temperature Range °C |
Total |
Reversing μm / m °C |
Non-Reversing |
| 0 – 40 | 127.6 | 45.46 | 82.18 |
| 40 – 80 | 137.3 | 55.65 | 81.66 |
| 80 – 100 | 149.1 | 63.37 | 85.76 |
Separating the expansion into reversing and non-reversing components has obvious advantages. Polymer blends, copolymers, co-extrusions, and polymeric modifiers will likely respond differently to stretching during processing, which is observed in the non-reversing expansion. The sample will also have reversing expansion properties that can be evaluated separately including inherent isotropic properties. Another example are fillers that impart expansion properties not affected by the stretching process that will be dependent on the filler morphology.
Conclusions
The effects of processing or stretching a PP battery separator are found in the non-reversing dimension signal of MTMA which contains the time and temperature dependent (kinetic) dimension change. The data obtained in this investigation shows that the non-reversing dimension component is the main contributor to the overall dimension change in both the TD and MD.
MTMA may also be extended to other film structures and compositions; biaxially stretched films, co-extrusions, copolymers and blends are examples. Due to the kinetic nature of the non-reversing expansion, the effect of thermal cycling through the operating temperature range is potentially another important area of investigation.
The reversing dimension change contains the temperature dependent component which accounts for the inherent expansion properties including anisotropy. This would also be equally important in evaluating different film structures and compositions as well as inorganic components like fillers.
References
1. D. Price, “Theory and Applications of Modulated Temperature Programming to Thermomechanical Techniques,” Journal of Thermal Analysis and Calorimetry, vol. 64, pp. 323-330, 2001.
2. Roger Blaine, “Modulated Thermal Mechanical Analysis – Measuring Expansion and Contraction Simultaneously (TA311),” New Castle DE.
3. “ASTM E831 Standard Test for Linear Thermal Expansion of Solid Materials by Thermomechanical Analysis,” ASTM, West Conshohocken PA, 2006.
4. H Lau, J Browne, “Thermal Analysis of a Battery Separator (TA457),” TA Instruments, New Castle DE, 2022.
5. P. Castejon, “Polypropylene Based Porous Membranes: Influence of Polymer Composition, Extrusion Draw Ratio, and Uniaxial Strain,” Polymers, vol. 10, no. 33, 2010.
6. C. Love, “Thermomechanical Analysis and Durability of Commercial Micro-Porous Polymer Li-ion Battery Separators,” Journal of Power Sources, vol. 196, pp. 2905-2912, 2011.
7. C. Xie, “Stretched Induced Coil Helix Transition in Isotactic Polypropylene: A Molecular Dynamics Simulation,” Macromolecules, vol. 51, pp. 3994-4002, 15 May 2018.
8. F. Sadeghi, “Properties of Uniaxially Stretched Polypropylene Films: Effects of Drawing Temperature and Random Copolymer Content,” The Canadian Journal of Chemical Engineering, vol. 88, December 2010.
Acknowledgement
This paper was written by James Browne and Hang Lau, Ph.D. at TA Instruments.
TA Instruments has been long recognized as an innovator and leader in modulated thermal analysis.
Click here to download the printable version of this application note.

